题目内容
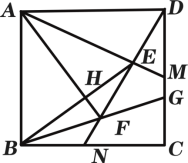
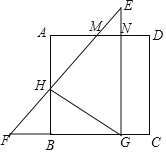
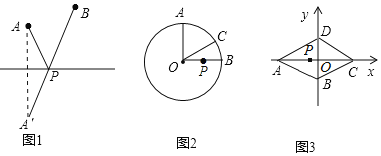
【题目】阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题﹣﹣如图1,从A点出发,到笔直的河岸l去饮马,然后再去B地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B 的值最小.
解答问题:
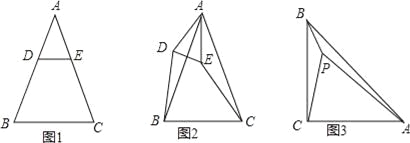
(1)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(2)如图3,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.
①为使点P能在最短的时间内到达点B处,则点M的位置应如何确定?
②在①的条件下,设点P的运动时间为t(s),△PAB的面积为S,在整个运动过程中,试求S与t之间的函数关系式,并指出自变量t的取值范围.
【答案】(1)PA+PC的最小值是2![]() ;(2)①点M的位置是(
;(2)①点M的位置是(![]() ,0)时,用时最少;②S与t之间的函数关系式是当3
,0)时,用时最少;②S与t之间的函数关系式是当3![]() <t≤4
<t≤4![]() 时,S=18
时,S=18![]() ﹣3t;当0<t≤3
﹣3t;当0<t≤3![]() 时,S=3t.当4
时,S=3t.当4![]() <t≤6
<t≤6![]() 时,S=﹣3t+18
时,S=﹣3t+18![]() .
.
【解析】
(1)延长AO交圆O于M,连接CM交OB于P,连接AC,AP+PC=PC+PM=CM最小;
(2)①根据运动速度不同以及运动距离,得出当PB⊥AB时,点P能在最短的时间内到达点B处;
②根据三角形的面积公式求出从A到C时,s与t的关系式和从C到(![]() ,0)以及到B的解析式.
,0)以及到B的解析式.
解:(1)延长AO交圆O于M,连接CM交OB于P,连接AC,
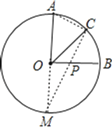
则此时AP+PC=PC+PM=CM最小,
∵AM是直径,∠AOC=60°,
∴∠ACM=90°,∠AMC=30°,
∴AC=![]() AM=2,AM=4,由勾股定理得:CM=
AM=2,AM=4,由勾股定理得:CM=![]() =2
=2![]() .
.
答:PA+PC的最小值是2![]() .
.
(2)①根据动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动,即为使点P能在最短的时间内到达点B处,
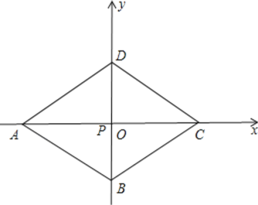
∴当PB⊥AB时,根据垂线段最短得出此时符合题意,
∵菱形ABCD,AB=6,∠DAB=60°,
∴∠BAO=30°,AB=AD,AC⊥BD,
∴△ABD是等边三角形,
∴BD=6,BO=3,由勾股定理得:AO=3![]() ,
,
在Rt△APB中,AB=6,∠BAP=30°,BP=![]() AP,由勾股定理得:AP=4
AP,由勾股定理得:AP=4![]() ,BP=2
,BP=2![]() ,
,
∴点M的位置是(![]() ,0)时,用时最少.
,0)时,用时最少.
②当0<t≤3![]() 时,AP=2t,
时,AP=2t,
∵菱形ABCD,
∴∠OAB=30°,
∴OB=![]() AB=3,
AB=3,
由勾股定理得:AO=CO=3![]() ,
,
∴S=![]() AP×BO=
AP×BO=![]() ×2t×3=3t;
×2t×3=3t;
③当3![]() <t≤4
<t≤4![]() 时,AP=6
时,AP=6![]() ﹣(2t﹣6
﹣(2t﹣6![]() )=12
)=12![]() ﹣2t,
﹣2t,
∴S=![]() AP×BO=
AP×BO=![]() ×(12
×(12![]() ﹣2t)×3=18
﹣2t)×3=18![]() ﹣3t.
﹣3t.
当4![]() <t≤6
<t≤6![]() 时,
时,
S=![]() AB×BP=
AB×BP=![]() ×6×[2
×6×[2![]() ﹣(t﹣4
﹣(t﹣4![]() )]=﹣3t+18
)]=﹣3t+18![]() ,
,
答:S与t之间的函数关系式是当3![]() <t≤4
<t≤4![]() 时,S=18
时,S=18![]() ﹣3t;当0<t≤3
﹣3t;当0<t≤3![]() 时,S=3t.当4
时,S=3t.当4![]() <t≤6
<t≤6![]() 时,S=﹣3t+18
时,S=﹣3t+18![]() .
.

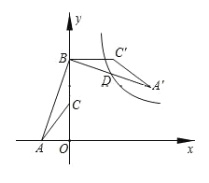
【题目】如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A′BC′,若反比例函数![]() 的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
的图像恰好经过A′B的中点D,求这个反比例函数的解析式.
【题目】某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后郗进行了测试.现将项目选择情况及训练前后篮球定时定点投测试成绩整理作出如下统计图表.
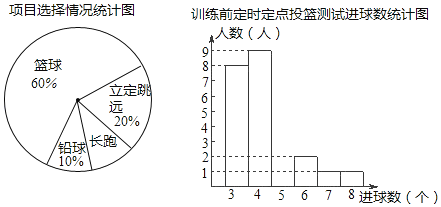
训练后篮球定时定点投篮测试进球数统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题
(1)送择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(2)直接补全“训练前篮球定时定点投测试进球数统计图”;
(3)若全区共有该年级学生4000人,请估计参加训练后篮球定时定点投篮进球数达到6个以上(包含6个)多少人?