题目内容
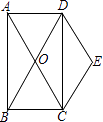
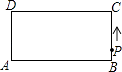
【题目】如图,1,将一张矩形纸片![]() 沿着对角线
沿着对角线![]() 向上折叠,顶点
向上折叠,顶点![]() 落到点
落到点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等腰三角形;
是等腰三角形;
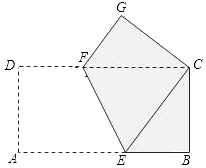
(2)如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() .
.
①判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】
试题分析: (1)根据两直线平行内错角相等及折叠特性判断;
(2)①根据已知矩形性质及第一问证得邻边相等判断;
②根据折叠特性设未知边,构造勾股定理列方程求解.
试题解析:(1)证明:如图1,根据折叠,∠DBC=∠DBE,

又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵FD∥BG,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=![]() BD=5.
BD=5.
假设DF=BF=x,∴AF=AD﹣DF=8﹣x.
∴在直角△ABF中,AB2+A2=BF2,即62+(8﹣x)2=x2,
解得x=![]() ,
,
即BF=![]() ,
,
∴FO=![]() =
=![]() ,
,
∴FG=2FO=![]() .
.


练习册系列答案
相关题目
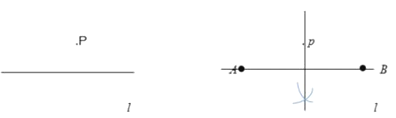
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
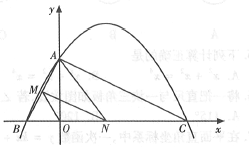
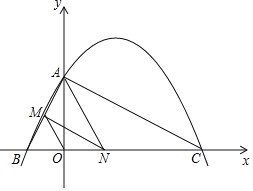
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)