Question

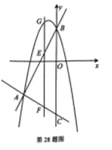
【题目】如图，抛物线与直线交于，两点，直线交轴与点，点是直线上的动点，过点作轴交于点，交抛物线于点.

(1)求抛物线的表达式；

(2)连接，，当四边形是平行四边形时，求点的坐标；

(3)①在轴上存在一点，连接，，当点运动到什么位置时，以为顶点的四边形是矩形？求出此时点的坐标；

②在①的前提下，以点为圆心，长为半径作圆，点为上一动点，求的最小值.

Answer 1

【答案】(1) y=﹣x2﹣2x+4；(2) G（﹣2，4）；(3)①E（﹣2，0）．H（0，﹣1）；②．

【解析】

试题分析: （1）利用待定系数法求出抛物线解析式；

（2）先利用待定系数法求出直线AB的解析式，进而利用平行四边形的对边相等建立方程求解即可；

（3）①先判断出要以点A，E，F，H为顶点的四边形是矩形，只有EF为对角线，利用中点坐标公式建立方程即可；

②先取EG的中点P进而判断出△PEM∽△MEA即可得出PM=AM，连接CP交圆E于M，再求出点P的坐标即可得出结论．

试题解析：（1）∵点A（﹣4，﹣4），B（0，4）在抛物线y=﹣x2+bx+c上，

∴，

∴，

∴抛物线的解析式为y=﹣x2﹣2x+4；

（2）设直线AB的解析式为y=kx+n过点A，B，

∴ ，

∴，

∴直线AB的解析式为y=2x+4，

设E（m，2m+4），

∴G（m，﹣m2﹣2m+4），

∵四边形GEOB是平行四边形，

∴EG=OB=4，

∴﹣m2﹣2m+4﹣2m﹣4=4，

∴m=﹣2，

∴G（﹣2，4）；

（3）①如图1，

由（2）知，直线AB的解析式为y=2x+4，

∴设E（a，2a+4），

∵直线AC：y=﹣x﹣6，

∴F（a，﹣a﹣6），

设H（0，p），

∵以点A，E，F，H为顶点的四边形是矩形，

∵直线AB的解析式为y=2x+4，直线AC：y=﹣x﹣6，

∴AB⊥AC，

∴EF为对角线，

∴（﹣4+0）=（a+a），（﹣4+p）=（2a+4﹣a﹣6），

∴a=﹣2，P=﹣1，

∴E（﹣2，0）．H（0，﹣1）；

②如图2，

由①知，E（﹣2，0），H（0，﹣1），A（﹣4，﹣4），

∴EH=，AE=2，

设AE交⊙E于G，取EG的中点P，

∴PE=，

连接PC交⊙E于M，连接EM，

∴EM=EH=，

∴=，

∵=，

∴，

∵∠PEM=∠MEA，

∴△PEM∽△MEA，

∴，

∴PM=AM，

∴AM+CM的最小值=PC，

设点P（p，2p+4），

∵E（﹣2，0），

∴PE2=（p+2）2+（2p+4）2=5（p+2）2，

∵PE=，

∴5（p+2）2=，

∴p=﹣或p=﹣（由于E（﹣2，0），所以舍去），

∴P（﹣，﹣1），

∵C（0，﹣6），

∴PC=，

即：AM+CM=．