题目内容
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
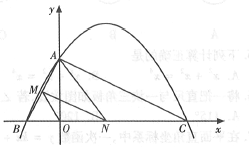
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,若点
,若点![]() 在线段
在线段![]() 上运动(不与点
上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 面积最大时,求N点的坐标;
面积最大时,求N点的坐标;
(3)连接![]() ,在(2)的结论下,求
,在(2)的结论下,求![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)![]() ;(2)N(3,0);(3)
;(2)N(3,0);(3)![]() .
.
【解析】
试题分析:(1)把点B,C的坐标代入到![]() ,求出a,b的值;(2)设N(n,0),用含n的代数式表示出△ABN的面积,利用AM与AB的比,用含n的代数式表示出△AMN的面积,根据二次函数的性质确定n的值;(3)因为点N是OC的中点,从而M是AB的中点,在直角三角形ABO中求出OM,在直角三角形AOC求出AC,即可解题.
,求出a,b的值;(2)设N(n,0),用含n的代数式表示出△ABN的面积,利用AM与AB的比,用含n的代数式表示出△AMN的面积,根据二次函数的性质确定n的值;(3)因为点N是OC的中点,从而M是AB的中点,在直角三角形ABO中求出OM,在直角三角形AOC求出AC,即可解题.
试题解析:(1)将点B,点C的坐标分别代入![]() ,
,
得:![]() ,解得:
,解得:![]() ,
,![]() .
.
∴该二次函数的表达式为![]() .
.
(2)设点N的坐标为(n,0)(-2<n<8),
则![]() ,
,![]() .
.
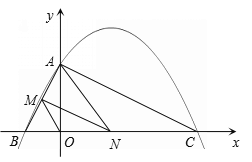
∵B(-2,0), C(8,0), ∴BC=10.
令x=0,解得:y=4,
∴点A(0,4),OA=4,
∵MN∥AC,
∴![]() .
.

∴![]()
∴当n=3时,即N(3,0)时,△AMN的面积最大.
(3)当N(3,0)时,N为BC边中点.
∴M为AB边中点,∴![]()
∵![]() ,
,
![]() ,
,
∴![]()
∴![]() .
.

练习册系列答案
相关题目


