题目内容
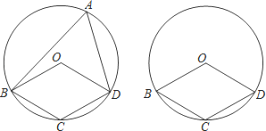
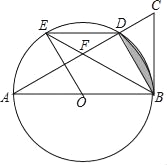
【题目】如图，在△ABC中，∠C=90°，∠A=25°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E，则
的度数为（ ）
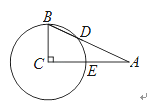
A. 25° B. 30° C. 50° D. 65°
【答案】C
【解析】
试题因为弧与垂径定理有关；与圆心角、圆周角有关；与弦、弦心距有关；弧与弧之间还存在着和、差、倍、半的关系，因此这道题有很多解法，仅选几种供参考．
解法一：（用垂径定理求）
如图，过点C作CF⊥AB于点G，交
于点G，
∴
，
又∵∠ACB=90°，∠A=25°，
∴∠GCB=25°，
∴的度数为25°，
∴的度数为50°；
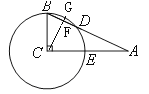
解法二：（用圆周角求）如图，延长BC交⊙C于点F，连接FD，
∵BF是直径，
∴∠BDF=90°，
∵∠ACB=90°，∠A=25°，
∴∠F=∠A=25°，
∴的度数为50°；
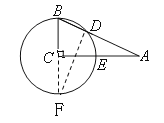
解法三：（用圆心角求）如图，连接CD，
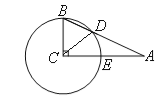
∵∠ACB=90°，∠A=25°，
∴∠B=65°，
∵CA=CD，
∴∠BDC=∠B=65°
∴∠ACD=50°，
∴的度数为50°
考点: 圆心角、弧、弦的关系,垂径定理．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
