题目内容
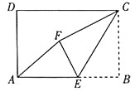
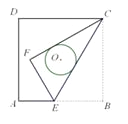
【题目】如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
连接CO,由O点是正方形的中心可知,∠DCO=∠BCO;由切线长定理可知∠FCO=∠ECO,则∠DCF=∠DCO-∠FCO=∠BCO-∠ECO=∠BCE,即∠DCF=∠BCE,由翻折可得∠ECF=∠BCE,故可得∠DCF=∠BCE=∠ECF,据此进行解答即可.
解:连接CO,
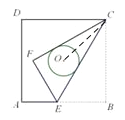
由于点O是正方形ABCD的中心,故∠DCO=∠BCO=45°;CF、CE为圆心的⊙O切线,则根据切线长定理可知∠FCO=∠ECO,则∠DCF=∠DCO-∠FCO=∠BCO-∠ECO=∠BCE,即∠DCF=∠BCE.再根据题干条件,将△BCE沿CE折叠至△FCE,则∠ECF=∠BCE,故可得:
∠DCF=∠BCE=∠ECF=![]() ,在RT△BCE中,CE=
,在RT△BCE中,CE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目