��Ŀ����
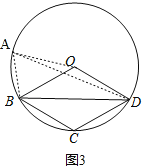
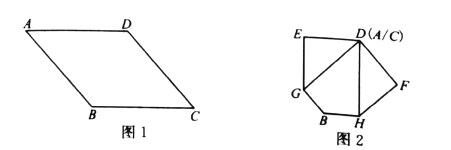
����Ŀ����ͼ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ�����㣨�����B��C��D�غϣ���
��1������A���Ż�![]() �ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
�ϣ���Բ��O�ڡ�BAD���ڲ�����֪��BOD=120�������OBA+��ODA= �㣮
��2�����ı���OBCDΪƽ���ı��Σ�
�ٵ�Բ��O�ڡ�BAD���ڲ�ʱ�����OBA+��ODA�Ķ�����
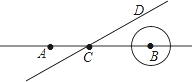
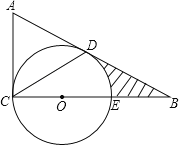
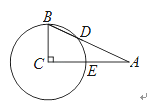
�ڵ�Բ��O�ڡ�BAD���ⲿʱ���뻭��ͼ�β�ֱ��д����OBA���ODA��������ϵ��
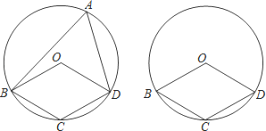
���𰸡���1��60������2����60�����ڡ�OBA=��ODA+60����
��������
���⣨1������BD������Բ�ܽǶ����������BAD�Ķ����Ƕ��٣�Ȼ����������ε��ڽǺͶ����������0BD����ODB�Ķ������Ƕ��٣��������ABD�У���180����ȥ��BAD����0BD����ODB�Ķ����ͣ������OBA+��ODA���ڶ��ټ��ɣ�
��2�������ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������ƽ���ı��ε����ʣ������OBC����ODC�Ķ������ٸ�����ABC+��ADC=180���������OBA+��ODA���ڶ��ټ��ɣ�
�����ȸ����ı���OBCDΪƽ���ı��Σ��ɵ���BOD=��BCD����OBC=��ODC��Ȼ�������BAD+��BCD=180������BAD=![]() ��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
��B0D�������B0D�Ķ��������������BAD�Ķ�����������OA=OD��OA=OB���жϳ���OAD=��ODA����OAB=��OBA�������жϳ���OBA=��ODA+60�����ɣ�
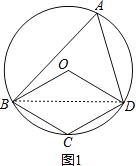
����������⣺��1����ͼ1������BD��
�ߡ�BOD=120����
���BAD=120���2=60����
���0BD+��ODB=180�㩁��BOD=180�㩁120��=60����
���OBA+��ODA=180�㩁����0BD+��ODB������BAD=180�㩁60�㩁60��=120�㩁60��=60����
�ʴ�Ϊ��60��
��2������ͼ2��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OBC=��ODC=180�㩁120��=60����
���ߡ�ABC+��ADC=180����
���OBA+��ODA=180�㩁����OBC+��ODC��=180�㩁��60��+60����=180�㩁120��=60����
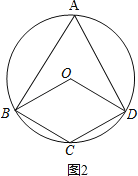
����ͼ3��
���ı���OBCDΪƽ���ı��Σ�
���BOD=��BCD����OBC=��ODC��
���ߡ�BAD+��BCD=180������BAD=![]() ��B0D��
��B0D��
��![]() ��B0D+��B0D=180����
��B0D+��B0D=180����
���B0D=120������BAD=120���2=60����
���OAB=��OAD+��BAD=��OAD+60����
��OA=OD��OA=OB��
���OAD=��ODA����OAB=��OBA��
���OBA=��ODA+60����