Question

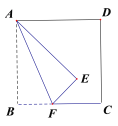
【题目】如图，在正方形ABCD中，将正方形ABCD沿AF折叠，使点B落在点E处.已知AB=4cm,BF=1cm,则点E到CD的距离为________cm.

Answer 1

【答案】cm.

【解析】

作辅助线过点E作GH∥CD,交BC于点H,AD于点G,证明△AGE∽△EHF,得,根据已知线段长度求出AG长,即可解题.

解：过点E作GH∥CD,交BC于点H,AD于点G.

∵四边形ABCD是正方形,

∴∠AGE=∠EHF=90°,

由折叠可知∠A=∠AEF=90°,

∴∠GAE=∠HEF（同角的余角相等）

∴△AGE∽△EHF.

∴,

∵AB=4cm,BF=1cm,设HF=xcm,

∴AE=4,EF=1,AG=1+x,

∴,

∴GE=4x,EH=,

∴4x+=4,解得：x=,

∴AG=

∴GD=

∴点E到CD的距离为cm.