��Ŀ����
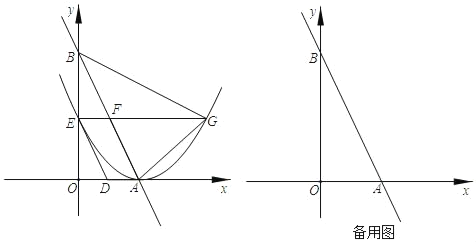
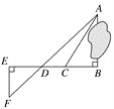
����Ŀ����֪��ABC�DZ߳�Ϊ4�ĵȱ������Σ���AB������OM�ϣ���OA��6����D������OM�ϵĶ��㣬����D�����A�غ�ʱ������ACD�Ƶ�C��ʱ�뷽����ת60��õ���BCE������DE����OD��m��
(1)���ⷢ��
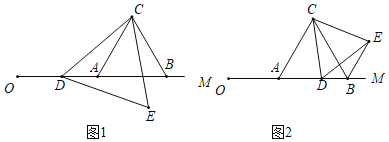
��ͼ1����CDE����״���� �������Σ�
(2)̽��֤��
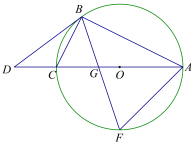
��ͼ2����6��m��10ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE�ܳ�����Сֵ���������ڣ���˵�����ɣ�
(3)�������
�Ƿ����m��ֵ��ʹ��DEB��ֱ�������Σ������ڣ���ֱ��д��m��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)�ȱߣ�(2)���ڣ���6��t��10ʱ����BDE����С�ܳ�2![]() +4��(3)��m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�
+4��(3)��m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�
��������
��1������ת�����ʵõ���DCE��60����DC��EC�����ɵõ����ۣ�
��2����6��m��10ʱ������ת�����ʵõ�BE��AD�����ǵõ�C��DBE��BE+DB+DE��AB+DE��4+DE�����ݵȱ������ε����ʵõ�DE��CD���ɴ��߶���̵õ���CD��ABʱ����BDE���ܳ���С�����ǵõ����ۣ�
��3�����ڣ��ٵ���D���B�غ�ʱ��D��B��E���ܹ��������Σ�
�ڵ�0��m��6ʱ������ת�����ʵõ���ABE��60������BDE��60������á�BED��90�������ݵȱ������ε����ʵõ���DEB��60������á�CEB��30�������OD��OA��DA��6��4��2��m
�۵�6��m��10ʱ����ʱ�����ڣ�
�ܵ�m��10ʱ������ת�����ʵõ���DBE��60������á�BDE��60�������ǵõ�m��14��
(1)�߽���ACD�Ƶ�C��ʱ�뷽����ת60���õ���BCE��
���DCE��60����DC��EC��
���CDE�ǵȱ������Σ�
�ʴ�Ϊ���ȱߣ�
(2)���ڣ���6��t��10ʱ��
����ת�����ʵã�BE��AD��
��C��DBE��BE+DB+DE��AB+DE��4+DE��
��(1)֪����CDE�ǵȱ������Σ�
��DE��CD��
��C��DBE��CD+4��
�ɴ��߶���̿�֪����CD��ABʱ����BDE���ܳ���С��
��ʱ��![]()
���BDE����С�ܳ�![]()
(3)���ڣ��١ߵ���D���B�غ�ʱ��D��B��E���ܹ��������Σ�
�൱��D���B�غ�ʱ�����������⣬
�ڵ�0��m��6ʱ������ת��֪����ABE��60������BDE��60����
���BED��90����
��(1)��֪����CDE�ǵȱ������Σ�
���DEB��60����
���CEB��30����
�ߡ�CEB����CDA��
���CDA��30����
�ߡ�CAB��60����
���ACD����ADC��30����
��DA��CA��4��
��OD��OA��DA��6��4��2��
��m��2��
�۵�6��m��10ʱ���ɡ�DBE��120����90����
���ʱ�����ڣ�
�ܵ�m��10ʱ������ת�����ʿ�֪����DBE��60����
����(1)֪��CDE��60����
���BDE����CDE+��BDC��60��+��BDC��
����BDC��0����
���BDE��60����
��ֻ�ܡ�BDE��90����
�Ӷ���BCD��30����
��BD��BC��4��
��OD��14��
��m��14��
������������m��2��14ʱ����D��E��BΪ�������������ֱ�������Σ�

����Ŀ��ij��ѧΪ�˿�ѧ������ѧ�������ɳ��������������ȡ�˲���ѧ����ͥ����ҳ�����������Ϊ����ĩ�����ڼ��������������ʾ����飬�����յ��ʾ����з����������õ������µ�����ͳ�Ʊ�������ͳ��ͼ��
���� | ������� | ��ͥ�� |
| �������沢�ҹ�������ҵ������ | 16 |
| ֻ��������ҵ������ | b |
| ֻ�������� | 8 |
| �Ȳ���������Ҳ����������ҵ������ | d |
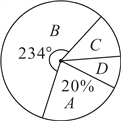
��1����![]() ��ֵ��
��ֵ��
��2����Уѧ����ͥ����Ϊ500��ѧУ������������![]() ���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ
���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ![]() ��ȡ20%��
��ȡ20%��![]() ���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
��3������![]() ���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������
���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������![]() ����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�