Question

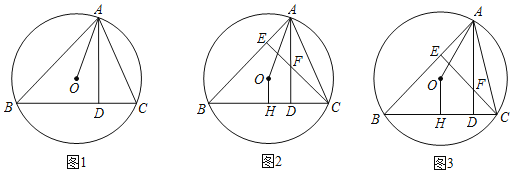
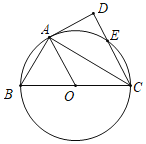
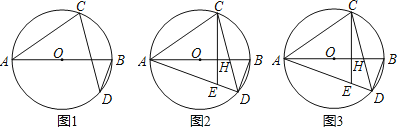
【题目】如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．

（1）若∠ABD＝α，求∠BDC（用α表示）；

（2）过点C作CE⊥AB于H，交AD于E，∠CAD＝β，求∠ACE（用β表示）；

（3）在（2）的条件下，若OH＝5，AD＝24，求线段DE的长．

Answer 1

【答案】（1）∠BDC=α；（2）∠ACE=β；（3）DE=．

【解析】

（1）连接AD，设∠BDC＝γ，∠CAD＝β，则∠CAB＝∠BDC＝γ，证明∠DAB＝βγ，β＝90°γ，∠ABD＝2γ，得出∠ABD＝2∠BDC，即可得出结果；

（2）连接BC，由直角三角形内角和证明∠ACE＝∠ABC，由点C为弧ABD中点，得出∠ADC＝∠CAD＝∠ABC＝β，即可得出结果；

（3）连接OC，证明∠COB＝∠ABD，得出△OCH∽△ABD，则＝＝，求出BD＝2OH＝10，由勾股定理得出AB＝＝26，则AO＝13，AH＝AO＋OH＝18，证明△AHE∽△ADB，得出＝，求出AE＝，即可得出结果．

（1）连接AD，如图1所示：

设∠BDC＝γ，∠CAD＝β，

则∠CAB＝∠BDC＝γ，

∵点C为弧ABD中点，

∴，

∴∠ADC＝∠CAD＝β，

∴∠DAB＝β﹣γ，

∵AB为⊙O直径，

∴∠ADB＝90°，

∴γ+β＝90°，

∴β＝90°﹣γ，

∴∠ABD＝90°﹣∠DAB＝90°﹣（β﹣γ）＝90°﹣90°+γ+γ＝2γ，

∴∠ABD＝2∠BDC，

∴∠BDC＝∠ABD＝α；

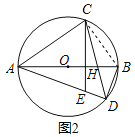
（2）连接BC，如图2所示：

∵AB为⊙O直径，

∴∠ACB＝90°，即∠BAC+∠ABC＝90°，

∵CE⊥AB，

∴∠ACE+∠BAC＝90°，

∴∠ACE＝∠ABC，

∵点C为弧ABD中点，

∴，

∴∠ADC＝∠CAD＝∠ABC＝β，

∴∠ACE＝β

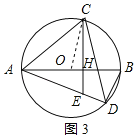
（3）连接OC，如图3所示：

∴∠COB＝2∠CAB，

∵∠ABD＝2∠BDC，∠BDC＝∠CAB，

∴∠COB＝∠ABD，

∵∠OHC＝∠ADB＝90°，

∴△OCH∽△ABD，

∴＝＝，

∴BD＝2OH＝10，

∴AB＝＝＝26，

∴AO＝13，

∴AH＝AO+OH＝13+5＝18，

∵∠EAH＝∠BAD，∠AHE＝∠ADB＝90°，

∴△AHE∽△ADB，

∴＝，即＝，

∴AE＝，

∴DE＝AD﹣AE＝24﹣＝．