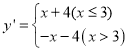Question

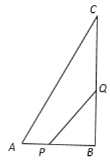
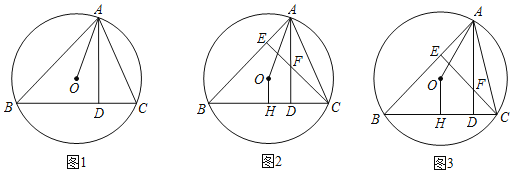
【题目】如图，在四边形中，点和点是对角线上的两点，且过点作交的延长线于点．

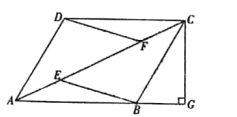
（1）求证：四边形是平行四边形．

（2）若，，BC=4，则的面积是

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据已知条件得到AF＝CE，根据平行线的性质得到∠DFA＝∠BEC，根据全等三角形的性质得到AD＝CB，∠DAF＝∠BCE，于是得到结论；

（2）根据已知条件得到△BCG是等腰直角三角形，求得BG、CG，解直角三角形得到AG，根据平行四边形的面积公式即可得到结论．

（1）证明：∵AE＝CF，

∴AE＋EF＝CF＋EF，

即AF＝CE，

∵DF∥BE，

∴∠DFA＝∠BEC，

∵DF＝BE，

∴△ADF≌△CBE（SAS），

∴AD＝CB，∠DAF＝∠BCE，

∴AD∥CB，

∴四边形ABCD是平行四边形；

（2）解：∵CG⊥AB，

∴∠G＝90，

∵∠CBG＝60，

∴∠BCG＝30

∵BC＝4，

∴BG＝2，CG＝6，

∵=，

即

∴AG＝8，

∴AB＝AG-BG=8-2=6，

∴平行四边形ABCD的面积＝6×6＝36，

故答案为：36．