Question

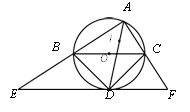
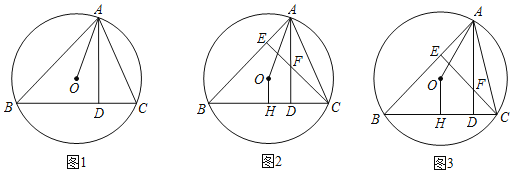
【题目】已知锐角△ABC内接于⊙O，AD⊥BC于点D，连接AO．

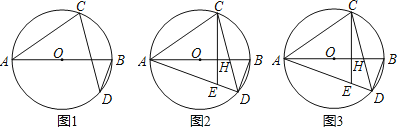
（1）如图1，求证：∠BAO＝∠CAD；

（2）如图2，CE⊥AB于点E，交AD于点F，过点O作OH⊥BC于点H，求证：AF＝2OH；

（3）如图3，在（2）的条件下，若AF＝AO，tan∠BAO＝，BC＝，求AC的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；+3．

【解析】

（1）延长AO交⊙O于K，连接BK．利用等角的余角相等证明即可．

（2）延长CO交⊙O于M，连接AM，BM，连接BF．证明四边形AMBF是平行四边形，BM＝2OH即可解决问题．

（3）延长CO交⊙O于M，连接AM，BM，连接BF．证明∠BAO＝∠DAC＝∠DBF，推出tan∠DBF＝tan∠BAP＝＝，设DF＝x，则BD＝3x，CD＝2﹣3x，AD＝6﹣9x，AF＝BM＝6﹣10x，构建方程即可解决问题．

（1）证明：延长AO交⊙O于K，连接BK．

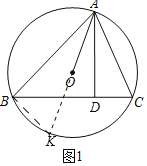
∵AK是直径，

∴∠ABK＝90°，

∵AD⊥BC，

∴∠ADC＝90°，

∵∠BAO+∠K＝90°，∠DAC+∠C＝90°，∠K＝∠C，

∴∠BAO＝∠DAC．

（2）证明：延长CO交⊙O于M，连接AM，BM，连接BF．

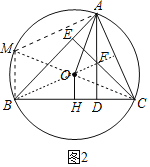
∵CM是直径，

∴∠CBM＝∠MAC＝90°，

∵OH⊥BC，

∴BH＝CH，∠OHC＝∠CBM＝90°，

∴AD∥BM，

∵OC＝OM，

∴BM＝2OH，

∵AD⊥BC，CA⊥AB，

∴BF⊥AC，∵A⊥AC，

∴AM∥BF，

∴四边形AMBF是平行四边形，

∴AF＝BM，

∴AF＝2OH．

（3）解：延长CO交⊙O于M，连接AM，BM，连接BF．

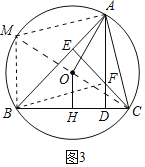
由（2）可知，四边形AMBF是平行四边形，

∴AF＝BM，

∴OA＝AF，

∴BM＝OA，

∴CM＝2BM，

∵∠CBM＝90°，

∴∠BCM＝30°，

∵∠BAO＝∠DAC＝∠DBF，

∴tan∠DBF＝tan∠BAP＝＝，设DF＝x，则BD＝3x，CD＝2﹣3x，AD＝6﹣9x，AF＝BM＝6﹣10x，

∵BC＝2，

∴BM＝BCtan30°＝2，

∴6﹣10x＝2，

∴x＝，

∴AC＝＝+3．