题目内容
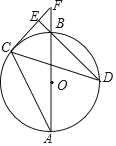
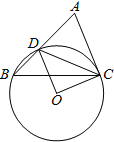
【题目】已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.如果∠ACB=75°,圆O的半径为2,则BD的长为_____.
【答案】2.
【解析】
接OB,根据∠DOC=2∠ACD=90°.得∠ACD=45°,进而得∠BCD=30°,∠BOC=150°,∠DOB=60°,证明△BOD是等边三角形,即可求得BD的长.
如图,连接OB,
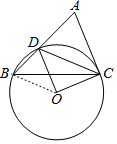
∵∠DOC=2∠ACD=90°.
∴∠ACD=45°,
∵∠ACB=75°,
∴∠BCD=∠ACB﹣∠ACD=30°,
∵OC=OD,∠DOC=90°,
∴∠DCO=45°,
∴∠BCO=∠DCO﹣∠BCD=15°,
∵OB=OC,
∴∠CBO=∠BCO=15°,
∴∠BOC=150°,
∴∠DOB=∠BOC﹣∠DOC=150°﹣90°=60°,
∵OB=OD,
∴△BOD是等边三角形,
∴BD=OD=2.
故答案为2.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?