题目内容
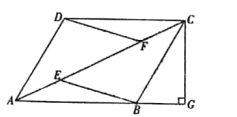
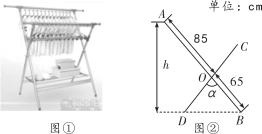
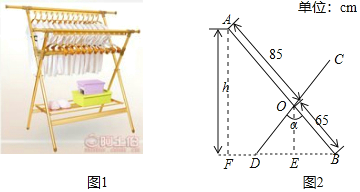
【题目】有一种落地晾衣架如图①所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图②是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85 cm,BO=DO=65 cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为______cm.(参考数据:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6)
【答案】120
【解析】
过O作OE⊥BD,过A作AF⊥BD,可得OE∥AF,利用等腰三角形的三线合一得到OE为角平分线,进而求出同位角的度数,在直角三角形AFB中,利用锐角三角函数定义求出h即可.
过O作OE⊥BD,过A作AF⊥BD,可得OE∥AF,
∵BO=DO,
∴OE平分∠BOD,
∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×74°=37°,
×74°=37°,
∴∠FAB=∠BOE=37°,
在Rt△ABF中,AB=85+65=150cm,
∴h=AF=ABcos∠FAB=150×0.8=120cm,
故答案为:120

练习册系列答案
相关题目