ΧβΡΩΡΎ»ί
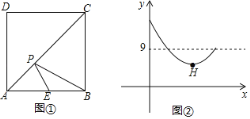
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC÷–Θ§ΓœB=90ΓψΘ§AB=12Θ§BC=16Θ§ΒψP¥”ΒψAΩΣ Φ―Ί±ΏABœρΒψB“‘1cm/sΒΡΥΌΕ»“ΤΕ·Θ§”κ¥ΥΆ§ ±Θ§ΒψQ¥”ΒψBΩΣ Φ―Ί±ΏBCœρΒψC“‘2cm/sΒΡΥΌΕ»“ΤΕ·Θ°»γΙϊPΓΔQΖ÷±π¥”AΓΔBΆ§ ±≥ωΖΔΘ§Β±ΒψQ‘ΥΕ·ΒΫΒψC ±Θ§ΝΫΒψΆΘ÷Ι‘ΥΕ·Θ§Έ ΘΚ
Θ®1Θ©Ψ≠ΙΐΦΗΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ20cm2ΘΩ
Θ®2Θ©ΓςPBQΒΡΟφΜΐΜαΒ»”ΎΓςABCΒΡΟφΜΐΒΡ“ΜΑκ¬πΘΩ»τΜαΘ§«κ«σ≥ω¥Υ ±ΒΡ‘ΥΕ· ±ΦδΘΜ»τ≤ΜΜαΘ§«κΥΒΟςάμ”….
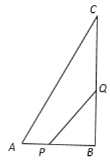
ΓΨ¥πΑΗΓΩΘ®1Θ©Ι Ψ≠Ιΐ2ΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ20 cm2ΘΜΘ®2Θ©≤ΜΜαΘ§ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΨ≠ΙΐtΟκΓςPBQΒΡΟφΜΐΒ»”Ύ20cm2Θ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΫ®ΝΔΖΫ≥Χ«σ≥ωΤδΫβΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨί»ΐΫ«–Έ÷°ΦδΒΡΟφΜΐΙΊœΒΫ®ΝΔΖΫ≥Χ«σ≥ωΤδΫβΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©“άΧβ“βΒΟ
AP=tȧBP=12-tȧBQ=2t
Γύ![]()
ΫβΒΟΘΚt1=2Θ§t2=10
ΓΏBQ=2tΓήBC=16
ΓύtΓή8
Γύt2=10…α»Ξ
Ι Ψ≠Ιΐ2ΟκΚσΘ§ΓςPBQΒΡΟφΜΐΒ»”Ύ20cm2ΘΜ
Θ®2Θ©≤ΜΜα
άμ”…ΘΚ»τΓςPBQΒΡΟφΜΐΜαΒ»”ΎΓςABCΒΡΟφΜΐΒΡ“ΜΑκΘ§”–
![]()
Γύ![]() Θ§
Θ§
ΓΏΓς=122-4ΓΝ48<0Θ§ΖΫ≥ΧΈό ΒΗυΘ§
“ρ¥ΥΓςPBQΒΡΟφΜΐ≤ΜΜαΒ»”ΎΓςABCΒΡΟφΜΐΒΡ“ΜΑκΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ