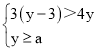Question

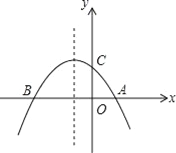
【题目】在平面直角坐标系中，直线经过点，与y轴交于点B，与抛物线的对称轴交于点．

（1）求m的值；

（2）求抛物线的顶点坐标；

（3）是线段AB上一动点，过点N作垂直于y轴的直线与抛物线交于点，（点P在点Q的左侧）．若恒成立，结合函数的图象，求a的取值范围．

Answer 1

【答案】（1）1；（2）．（3）．

【解析】

（1）将点A坐标代入求出，再根据直线过点即可求得的值；

（2）由（1）得出抛物线对称轴为，据此知 ，代入得，从而得出答案；

（3）当时，画出图形．若抛物线过点 知 ．结合函数图象可得 ．时显然不成立．

解：（1）∵ 经过点，

∴将点的坐标代入 ，即 ，得．

∵直线 与抛物线 的对称轴交于点 ，

∴将点代入，得 ．

(2)∵抛物线 的对称轴为，

∴ ，即．

∴

．

∴抛物线的顶点坐标为 ．

(3)当时，如图，

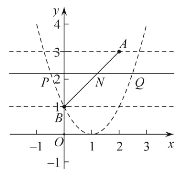
若拋物线过点 ，则 ．

结合函数图象可得 ．

当时，不符合题意．

综上所述，的取值范围是．