题目内容
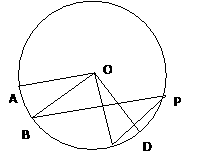
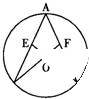
如图所示,点P在圆O上,将圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)。若∠AOC=β(0°<β<180°),则∠P的度数为(用α和β表示)( )

A.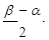 | B.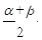 | C. | D.α+β |
A
根据圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°)可知∠AOB=α,再由∠AOC=β可求出∠COB的度数,根据圆周角定理即可求出∠P的度数.
解:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α-β,
∴∠P=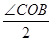 =
=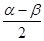 .
.
故选A.
本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.
解:∵圆心角∠AOC绕点O按逆时针旋转到∠BOD,旋转角为α(0°<α<180°),
∴∠AOB=α,
∵∠AOC=β,
∴∠COB=α-β,
∴∠P=
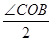 =
=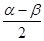 .
.故选A.
本题考查的是圆周角定理及图形的旋转,解答此题的关键是弄清旋转角即为∠AOB的度数.

练习册系列答案
相关题目
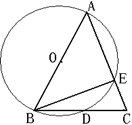
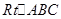 中,
中,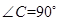 ,
,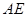 平分
平分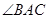 交
交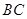 于
于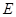 ,点
,点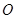 在
在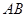 上,以
上,以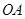 为半径的圆,交
为半径的圆,交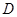 ,交
,交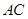 于
于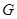 ,且点
,且点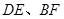 ,切⊙
,切⊙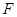
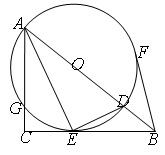
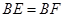
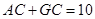 ,求⊙
,求⊙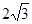 ,则∠EDC的度数为__▲ .
,则∠EDC的度数为__▲ .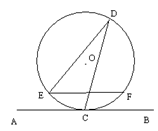
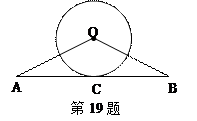
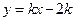 (
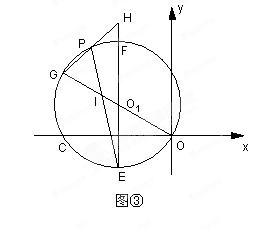
( )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A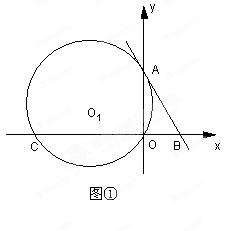
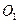 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
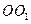 与⊙
与⊙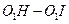 的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.