题目内容
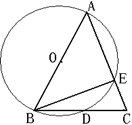
.已知;如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③ =;④AE=BC;其中正确结论的序号是__________.
 |
根据圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角等知识,运用排除法逐条分析判断.
解:连接OD,AD,OE,
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角),
∴AD⊥BC;
∵在△ABC中,AB=AC,
∴AD是边BC上的中线,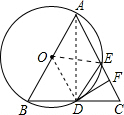
∴BD=DC,∠BAD=∠DAC,
∴劣弧DB=劣弧DE故②③正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=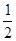 ∠BAC=22.5°,故①正确;
∠BAC=22.5°,故①正确;
故填:
本题利用了圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角求解.
解:连接OD,AD,OE,
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角),
∴AD⊥BC;
∵在△ABC中,AB=AC,
∴AD是边BC上的中线,

∴BD=DC,∠BAD=∠DAC,
∴劣弧DB=劣弧DE故②③正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=
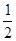 ∠BAC=22.5°,故①正确;
∠BAC=22.5°,故①正确;故填:
本题利用了圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角求解.

练习册系列答案
相关题目
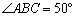 ,
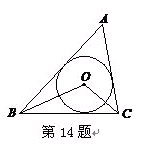
,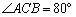 ,则
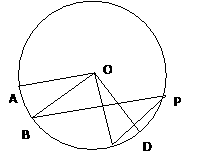
,则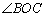 = °
= °



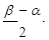
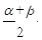

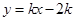 (
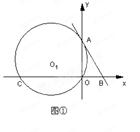
(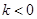 )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
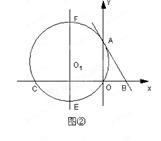
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.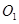 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
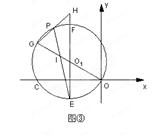
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;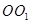 与⊙
与⊙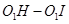 的值是否发生变化,若不变,求其值,若发
的值是否发生变化,若不变,求其值,若发 生
生 变化,求出其值的变化范围.
变化,求出其值的变化范围.