题目内容
如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C。问:线段CE和线段BF相等吗?请说明理由。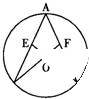

CE=BF
∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∵CE=OC+OE,BF=OB+OF,
∴CE=BF.
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∵CE=OC+OE,BF=OB+OF,
∴CE=BF.

练习册系列答案
相关题目
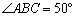 ,
,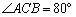 ,则
,则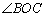 = °
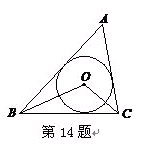
= °

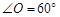 ,则
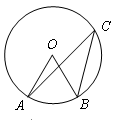
,则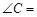 ( )
( )
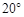 B.
B.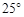 C.
C.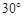 D.
D.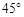
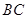 为
为 的弦,
的弦,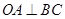 于
于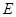 ,交
,交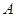 ,
,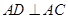 于
于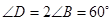 .
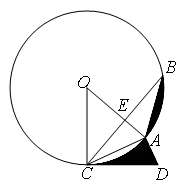
.
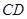 为
为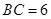 时,求阴影部分的面积
时,求阴影部分的面积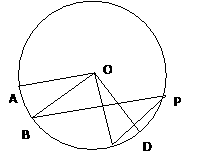
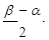
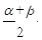

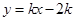 (
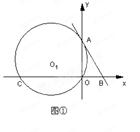
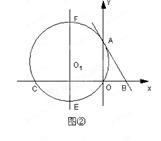
(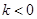 )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.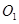 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;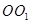 与⊙
与⊙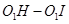 的值是否发生变化,若不变,求其值,若发
的值是否发生变化,若不变,求其值,若发 生
生 变化,求出其值的变化范围.
变化,求出其值的变化范围.