题目内容
如图,直线AB、CD相交于点O,∠AOC=300,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足条件 时,⊙P与直线CD相交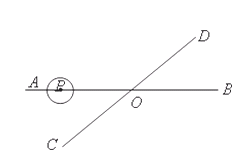

4<t<8;
分析:首先分析相切时的数量关系,则点P到CD的距离应是1,根据30°所对的直角边是斜边的一半,得OP=2;那么当点P在OA上时,需要运动(6-2)÷1=4秒;当点P在OB上时,需要运动(6+2)÷1=8秒.因为在这两个切点之间的都是相交,所以4<t<8.
解答:解:∵OP=6cm,
∴当点P在OA上时,需要运动(6-2)÷1=4秒,
当点P在OB上时,需要运动(6+2)÷1=8秒,
∵在这两个切点之间的都是相交,
∴4<t<8.
故答案为:4<t<8.
解答:解:∵OP=6cm,
∴当点P在OA上时,需要运动(6-2)÷1=4秒,
当点P在OB上时,需要运动(6+2)÷1=8秒,
∵在这两个切点之间的都是相交,
∴4<t<8.
故答案为:4<t<8.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目


 为
为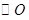 的弦,
的弦,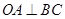 于
于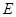 ,交
,交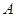 ,
,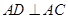 于
于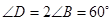 .
.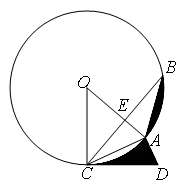
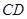 为
为 时,求阴影部分的面积
时,求阴影部分的面积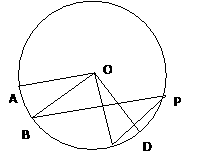
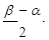
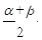

 ,那么∠A的度数为( )
,那么∠A的度数为( )