题目内容
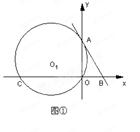
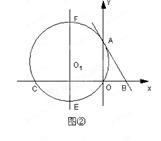
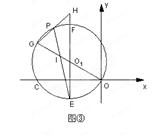
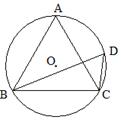
如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF//AB,若EF=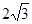 ,则∠EDC的度数为__▲ .
,则∠EDC的度数为__▲ .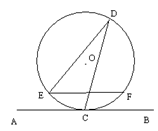
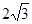 ,则∠EDC的度数为__▲ .
,则∠EDC的度数为__▲ .

分析:连接OC、OE,由切线的性质知OC⊥AB,而EF∥AB,则OC⊥EF;设OC交EF于M,在Rt△OEM中,根据垂径定理可得到EM的长,OE即⊙O的半径已知,即可求出∠EOM的正弦值,进而可求得∠EOM的度数,由圆周角定理即可得到∠EDC的度数.

解:连接OE、OC,设OC与EF的交点为M;
∵AB切⊙O于C,
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,则EM=MF= ;
;
Rt△OEM中,EM= ,OE=2;
,OE=2;
则sin∠EOM= ,∴∠EOM=60°;
,∴∠EOM=60°;
∴∠EDC= ∠EOM=30°.
∠EOM=30°.

解:连接OE、OC,设OC与EF的交点为M;
∵AB切⊙O于C,
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,则EM=MF=
 ;
;Rt△OEM中,EM=
 ,OE=2;
,OE=2;则sin∠EOM=
 ,∴∠EOM=60°;
,∴∠EOM=60°;∴∠EDC=
 ∠EOM=30°.
∠EOM=30°.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
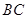 为
为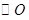 的弦,
的弦,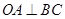 于
于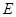 ,交
,交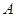 ,
,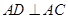 于
于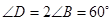 .
.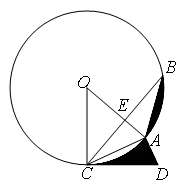
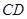 为
为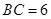 时,求阴影部分的面积
时,求阴影部分的面积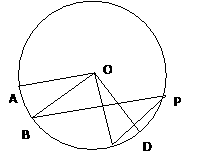
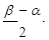
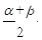

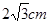 ,
,
 ,那么∠A的度数为( )
,那么∠A的度数为( )




 ; B、
; B、 ; C、3; D、
; C、3; D、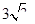 .
.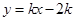 (
(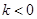 )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.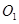 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;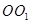 与⊙
与⊙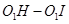 的值是否发生变化,若不变,求其值,若发
的值是否发生变化,若不变,求其值,若发 生
生 变化,求出其值的变化范围.
变化,求出其值的变化范围.