题目内容
【题目】阅读以下材料,并按要求完成相应的任务.
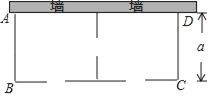
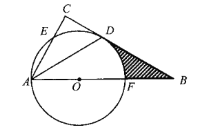
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?用现在的数学语言表达是:如图,![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为
,垂足为![]() ,
,![]() 寸,
寸,![]() 尺,其中1尺
尺,其中1尺![]() 寸,求出直径
寸,求出直径![]() 的长.
的长.
解题过程如下:
连接![]() ,设
,设![]() 寸,则
寸,则![]() 寸.
寸.
∵![]() 尺,∴
尺,∴![]() 寸.
寸.
在![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() 寸.
寸.
任务:
(1)上述解题过程运用了 定理和 定理.
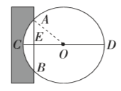
(2)若原题改为已知![]() 寸,
寸,![]() 尺,请根据上述解题思路,求直径
尺,请根据上述解题思路,求直径![]() 的长.
的长.
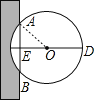
(3)若继续往下锯,当锯到![]() 时,弦
时,弦![]() 所对圆周角的度数为 .
所对圆周角的度数为 .
【答案】(1)垂径,勾股;(2)26寸;(3)![]() 或
或![]()
【解析】
(1)由解题过程可知根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,即可得到答案.
(2)连接OA,设OA=r寸,则OE=DE-r=25-r,再根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,进而得出结论.
(3)当AE=OE时,△AEO是等腰直角三角形,则∠AOE=45°,∠AOB=90°,所以由圆周角定理推知弦AB所对圆周角的度数为 45°或135°.
解:(1)根据题意知,上述解题过程运用了 垂径定理和 勾股定理.
故答案是:垂径;勾股;
(2)连接OA,设OA=r寸,则OE=DE-r=(25-r)寸
∵AB⊥CD,AB=1尺,∴AE=![]() AB=5寸
AB=5寸
在Rt△OAE中,OA2=AE2+OE2,即r2=52+(25-r)2,解得r=13,
∴CD=2r=26寸
(2)∵AB⊥CD,
∴当AE=OE时,△AEO是等腰直角三角形,
∴∠AOE=45°,
∴∠AOB=2∠AOE=90°,
∴弦AB所对圆周角的度数为![]() ∠AOB=45°.
∠AOB=45°.
同理,优弧AB所对圆周角的度数为135°.
故答案是:45°或135°.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目