题目内容
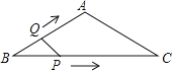
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
A.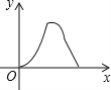 B.
B.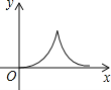 C.
C.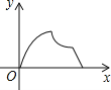 D.
D.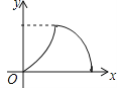
【答案】D
【解析】
作AH⊥BC于H,根据等腰三角形的性质得BH=CH,利用∠B=30°可计算出AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,BC=2BH=4
,BC=2BH=4![]() ,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类讨论:当0≤x≤2时,作QD⊥BC于D,如图1;当2<x≤4时,作QD⊥BC于D,如图2;于是可得0≤x≤2时,函数图象为抛物线的一部分,当2<x≤4时,函数图象为抛物线的一部分,即可得到答案.
,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类讨论:当0≤x≤2时,作QD⊥BC于D,如图1;当2<x≤4时,作QD⊥BC于D,如图2;于是可得0≤x≤2时,函数图象为抛物线的一部分,当2<x≤4时,函数图象为抛物线的一部分,即可得到答案.
解:如图1,作AH⊥BC于H,
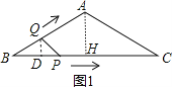
∵AB=AC=4cm,
∴BH=CH
∵∠B=30°,
∴AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,
,
∴BC=2BH=4![]() ,
,
∵点P运动的速度为![]() cm/s,Q点运动的速度为2cm/s,
cm/s,Q点运动的速度为2cm/s,
∴点P从B点运动到C需2![]() s,Q点运动到C需4s,
s,Q点运动到C需4s,
当0≤x≤2时,作QD⊥BC于D,如图1,BQ=2x,BP=![]() ,
,

在Rt△BPQ中,DQ=![]() BQ=x,
BQ=x,
∴y=![]() x
x![]() x=
x=![]() x2.
x2.
当2<x≤4时,作QD⊥BC于D,如图2,CQ=4-2x,BP=![]() x,
x,
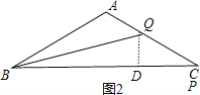
在Rt△BDQ中,DQ=![]() =
=![]() (4-2x),
(4-2x),
∴y=![]() (4-2x)
(4-2x)![]() =
=![]() ,
,
综上所述,y=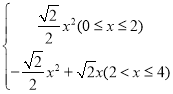
故选:D.

练习册系列答案
相关题目