ĖâÄŋÄÚČÝ
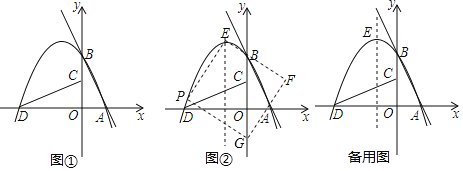
ĄūĖâÄŋĄŋŌŅÖŠÅŨÎïÏßyĢ―x2+ĢĻ2m+1ĢĐx+mĢĻmĐ3ĢĐĢŽĢĻmΊģĢĘýĢŽĐ1ĄÜmĄÜ4ĢĐĢŽAĢĻĐmĐ1ĢŽy1ĢĐĢŽ![]() ĘĮļÃÅŨÎïÏßÉÏēŧÍŽĩÄÁ―ĩãĢŽÏÖ―ŦÅŨÎïÏßĩÄķÔģÆÖáČÆŨøąęÔĩãOÄæĘąÕëÐýŨŠ90ĄãĩÃĩ―ÖąÏßaĢŽđýÅŨÎïÏßķĨĩãPŨũPHĄÍaÓÚHĢŪ
ĘĮļÃÅŨÎïÏßÉÏēŧÍŽĩÄÁ―ĩãĢŽÏÖ―ŦÅŨÎïÏßĩÄķÔģÆÖáČÆŨøąęÔĩãOÄæĘąÕëÐýŨŠ90ĄãĩÃĩ―ÖąÏßaĢŽđýÅŨÎïÏßķĨĩãPŨũPHĄÍaÓÚHĢŪ
ĢĻ1ĢĐĩąmĢ―1ĘąĢŽĮóģöÕâĖõÅŨÎïÏßĩÄķĨĩãŨøąęĢŧ
ĢĻ2ĢĐČôÎÞÂÛmČĄšÎÖĩĢŽÅŨÎïÏßÓëÖąÏßyĢ―xĐkmĢĻkΊģĢĘýĢĐÓÐĮŌ―öÓÐŌŧļöđŦđēĩãĢŽĮókĩÄÖĩĢŧ
ĢĻ3ĢĐĩą1ĢžPHĄÜ6ĘąĢŽĘÔąČ―Ïy1ĢŽy2ÖŪžäĩÄīóÐĄĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐĢĻĐ![]() ĢŽĐ
ĢŽĐ![]() ĢĐĢŧĢĻ2ĢĐk=3;ĢĻ3ĢĐĐ1ĄÜmĢžĐ
ĢĐĢŧĢĻ2ĢĐk=3;ĢĻ3ĢĐĐ1ĄÜmĢžĐ![]() ŧō
ŧō![]() ĢžmĄÜ
ĢžmĄÜ![]() ĘąĢŽÓÐy2Ģūy1ĢŽĐ
ĘąĢŽÓÐy2Ģūy1ĢŽĐ![]() ĢžmĢžĐ
ĢžmĢžĐ![]() ĘąĢŽÓÐy2Ģžy1
ĘąĢŽÓÐy2Ģžy1
Ąū―âÎöĄŋ
(1)ŧŊģÉķĨĩãĘ―žīŋÉĮóĩÃķĨĩãŨøąę;ĢĻ2ĢĐÁз―ģĖŨéļųūÝĄũ=0―âūöÎĘĖâ;ĢĻ3ĢĐĘŨÏČÖĪÃũy1=y3ĢŽÔŲļųūÝĩãBĩÄÎŧÖÃĢŽ·ÖĀāĖÖÂÛĢŽĒŲÁî![]() Ģž-m-1ĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÚÁî
Ģž-m-1ĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÚÁî![]() =-m-1ĢŽÔōAÓëBÖØšÏĢŽīËĮéÐÎēŧšÏĖâŌâĢŽÉáÆúĢŪĒÛÁî
=-m-1ĢŽÔōAÓëBÖØšÏĢŽīËĮéÐÎēŧšÏĖâŌâĢŽÉáÆúĢŪĒÛÁî![]() Ģū-m-1ĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÜÁî
Ģū-m-1ĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÜÁî![]() ĄÜ
ĄÜ![]() Ģž-mĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÝÁî
Ģž-mĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŽĒÝÁî![]() =-mĢŽBĢŽCÖØšÏĢŽēŧšÏĖâŌâÉáÆúĢŪĒÞÁî
=-mĢŽBĢŽCÖØšÏĢŽēŧšÏĖâŌâÉáÆúĢŪĒÞÁî![]() Ģū-mĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŪ
Ģū-mĢŽĮóģömĩÄ·ķΧžīŋÉÅÐķÏĢŪ
―âĢšĢĻ1ĢĐĄßmĢ―1ĢŽ
ĄāyĢ―x2+3xĐ2Ģ―ĢĻx+![]() ĢĐ2Đ
ĢĐ2Đ![]() ĢŽ
ĢŽ
ĄāķĨĩãŨøąęĢĻĐ![]() ĢŽĐ
ĢŽĐ![]() ĢĐĢŪ
ĢĐĢŪ
ĢĻ2ĢĐÓÉ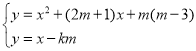 ÏûČĨyĩÃx2+2mx+ĢĻm2+kmĐ3mĢĐĢ―0ĢŽ
ÏûČĨyĩÃx2+2mx+ĢĻm2+kmĐ3mĢĐĢ―0ĢŽ
ĄßÅŨÎïÏßÓëÖąÏßyĢ―xĐkmÓÐĮŌ―öÓÐŌŧļöđŦđēĩãĢŽ
ĄāĄũĢ―0ĢŽžīĢĻkĐ3ĢĐmĢ―0ĢŽ
ĄßÎÞÂÛmČĄšÎÖĩĢŽ·―ģĖŨÜĘĮģÉÁĒĢŽ
ĄākĐ3Ģ―0ĢŽ
ĄākĢ―3ĢŪ
ĢĻ3ĢĐĄß![]() ĢŽ
ĢŽ
ÅŨÎïÏßyĢ―x2+ĢĻ2m+1ĢĐx+mĢĻmĐ3ĢĐĩÄķĨĩãΊ![]() ĢŽ
ĢŽ
PHĢ―|Đ![]() ĐĢĻĐ
ĐĢĻĐ![]() ĢĐ|Ģ―|
ĢĐ|Ģ―|![]() |ĢŽ
|ĢŽ
Ąß1ĢžPHĄÜ6ĢŽ
Ąāĩą![]() Ģū0ĘąĢŽÓÐ1Ģž
Ģū0ĘąĢŽÓÐ1Ģž![]() ĄÜ6ĢŽÓÖĐ1ĄÜmĄÜ4ĢŽ
ĄÜ6ĢŽÓÖĐ1ĄÜmĄÜ4ĢŽ
Ąā![]() ĢžmĄÜ
ĢžmĄÜ![]() ĢŽ
ĢŽ
ĩą![]() Ģž0ĘąĢŽ1ĢžĐ
Ģž0ĘąĢŽ1ĢžĐ![]() ĄÜ6ĢŽÓÖĄßĐ1ĄÜmĄÜ4ĢŽ
ĄÜ6ĢŽÓÖĄßĐ1ĄÜmĄÜ4ĢŽ
ĄāĐ1ĄÜmĢžĐ![]() ĢŽ
ĢŽ
ĄāĐ1ĄÜmĢžĐ![]() ŧō
ŧō![]() ĢžmĄÜ
ĢžmĄÜ![]() ĢŽ
ĢŽ
ĄßAĢĻĐmĐ1ĢŽy1ĢĐÔÚÅŨÎïÏßÉÏĢŽ
Ąāy1Ģ―ĢĻĐmĐ1ĢĐ2+ĢĻ2m+1ĢĐĢĻĐmĐ1ĢĐ+mĢĻm+3ĢĐĢ―Đ4mĢŽ
ĄßCĢĻĐmĢŽy3ĢĐÔÚÅŨÎïÏßÉÏĢŽ
Ąāy3Ģ―ĢĻĐmĢĐ2+ĢĻ2m+1ĢĐĢĻĐmĢĐ+mĢĻmĐ3ĢĐĢ―Đ4mĢŽ
Ąāy1Ģ―y3ĢŽ
ĒŲÁî![]() ĢžĐmĐ1ĢŽÔōÓÐmĢžĐ
ĢžĐmĐ1ĢŽÔōÓÐmĢžĐ![]() ĢŽ―ášÏĐ1ĄÜmĢžĐ
ĢŽ―ášÏĐ1ĄÜmĢžĐ![]() ĢŽ
ĢŽ
ĄāĐ1ĄÜmĢžĐ![]() ĢŽ
ĢŽ
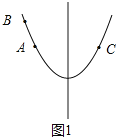
īËĘąĢŽÔÚķÔģÆÖáĩÄŨóēāyËæxĩÄÔöīóķøžõÐĄĢŽČįÍž1ĢŽ
Ąāy2Ģūy1Ģ―y3ĢŽ
žīĩąĐ1ĄÜmĢžĐ![]() ĘąĢŽÓÐy2Ģūy1Ģ―y3ĢŪ
ĘąĢŽÓÐy2Ģūy1Ģ―y3ĢŪ
ĒÚÁî![]() Ģ―ĐmĐ1ĢŽÔōAÓëBÖØšÏĢŽīËĮéÐÎēŧšÏĖâŌâĢŽÉáÆúĢŪ
Ģ―ĐmĐ1ĢŽÔōAÓëBÖØšÏĢŽīËĮéÐÎēŧšÏĖâŌâĢŽÉáÆúĢŪ
ĒÛÁî![]() ĢūĐmĐ1ĢŽĮŌ
ĢūĐmĐ1ĢŽĮŌ![]()
![]() ĘąĢŽÓÐĐ
ĘąĢŽÓÐĐ![]() ĢžmĄÜĐ
ĢžmĄÜĐ![]() ĢŽ―ášÏĐ1ĄÜmĢžĐ
ĢŽ―ášÏĐ1ĄÜmĢžĐ![]() ĢŽ
ĢŽ
ĄāĐ![]() ĢžmĄÜĐ
ĢžmĄÜĐ![]() ĢŽ
ĢŽ
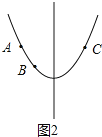
īËĘąĢŽÔÚķÔģÆÖáĩÄŨóēāĢŽyËæxĩÄÔöīóķøžõÐĄĢŽČįÍž2ĢŽ
Ąāy1Ģ―y3Ģūy2ĢŽ
žīĩąĐ![]() ĢžmĄÜĐ
ĢžmĄÜĐ![]() ĘąĢŽÓÐy1Ģ―y3Ģūy2ĢŽ
ĘąĢŽÓÐy1Ģ―y3Ģūy2ĢŽ
ĒÜÁî![]() ĢŽÓÐĐ
ĢŽÓÐĐ![]() ĄÜmĢž0ĢŽ―ášÏĐ1ĄÜmĢžĐ
ĄÜmĢž0ĢŽ―ášÏĐ1ĄÜmĢžĐ![]() ĢŽ
ĢŽ
ĄāĐ![]() ĄÜmĢžĐ
ĄÜmĢžĐ![]() ĢŽ
ĢŽ
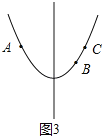
īËĘąĢŽÔÚķÔģÆÖáĩÄÓŌēāyËæxĩÄÔöīóķøÔöīóĢŽČįÍž3ĢŽ
Ąāy2Ģžy3Ģ―y1ĢŪ
ĒÝÁî![]() ĢŽBĢŽCÖØšÏĢŽēŧšÏĖâŌâÉáÆúĢŪ
ĢŽBĢŽCÖØšÏĢŽēŧšÏĖâŌâÉáÆúĢŪ
ĒÞÁî![]() ĢŽÓÐmĢū0ĢŽ―ášÏ
ĢŽÓÐmĢū0ĢŽ―ášÏ![]() ĢžmĄÜ
ĢžmĄÜ![]() ĢŽ
ĢŽ
Ąā![]() ĢžmĄÜ
ĢžmĄÜ![]() ĢŽ
ĢŽ
īËĘąĢŽÔÚķÔģÆÖáĩÄÓŌēāĢŽyËæxĩÄÔöīóķøÔöīóĢŽČįÍž4ĢŽ
Ąāy2Ģūy3Ģ―y1ĢŽ
žīĩą![]() ĢžmĄÜ
ĢžmĄÜ![]() ĘąĢŽÓÐy2Ģūy3Ģ―y1ĢŽ
ĘąĢŽÓÐy2Ģūy3Ģ―y1ĢŽ
ŨÛÉÏËųĘöĢŽĐ1ĄÜmĢžĐ![]() ŧō
ŧō![]() ĢžmĄÜ
ĢžmĄÜ![]() ĘąĢŽÓÐy2Ģūy1Ģ―y3ĢŽĐ
ĘąĢŽÓÐy2Ģūy1Ģ―y3ĢŽĐ![]() ĢžmĢžĐ
ĢžmĢžĐ![]() ĘąĢŽÓÐy2Ģžy1Ģ―y3ĢŪ
ĘąĢŽÓÐy2Ģžy1Ģ―y3ĢŪ


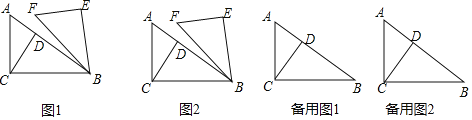
ĄūĖâÄŋĄŋĢĻÎĘĖâĖáģöĢĐČįđûīÓ![]() ĢŽ
ĢŽ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘý
ļöÁŽÐøĩÄŨÔČŧĘý![]() ĢŽÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ĢŽÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ĢĻÎĘĖâĖ―ūŋĢĐΊ·ĒÏÖđæÂÉĢŽÎŌÃĮēÉÓÃŌŧ°ãÎĘĖâĖØĘâŧŊĩÄēßÂÔĢŽÏČīÓŨîžōĩĨĩÄÎĘĖâČëĘÖĢŽÔŲÖðīÎĩÝ―øĢŽŨîšóĩÃģöŌŧ°ãÐÔĩÄ―áÂÛ.
Ė―ūŋŌŧĢšČįđûīÓ![]() ĢŽ
ĢŽ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽŧáÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ļöÁŽÐøĩÄŨÔČŧĘýĢŽŧáÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ĩą![]() ĢŽ
ĢŽ![]() ĘąĢŽÏÔČŧÓÐ
ĘąĢŽÏÔČŧÓÐ![]() ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
![]()
ĩą![]() ĢŽ
ĢŽ![]() ĘąĢŽÓÐ
ĘąĢŽÓÐ![]() ĢŽ
ĢŽ![]() Ģŧ
Ģŧ![]() ĢŽ
ĢŽ![]() Ģŧ
Ģŧ![]() ĢŽ
ĢŽ![]() Õâ
Õâ![]() ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
![]()
ĩą![]() ĢŽ
ĢŽ![]() ĘąĢŽÓÐ________ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ĘąĢŽÓÐ________ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ

ĄĄ
ÓÉÉÏŋÉÖŠĢšīÓ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
Ė―ūŋķþĢšČįđûīÓ![]() ĢŽ
ĢŽ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöĢŽ
ļöĢŽ![]() ļöĄĄ
ļöĄĄ![]()
![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽ·ÖąðÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ļöÁŽÐøĩÄŨÔČŧĘýĢŽ·ÖąðÓÐķāÉŲÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŋ
ÎŌÃĮ―čÖúÏÂÃæĩÄŋōÍžžĖÐøĖ―ūŋĢŽ·ĒÏÖđæÂÉēĒÓĶÓÃđæÂÉÍęģÉĖîŋÕ.
|
|
| ... |
|
|
|
|
|
|
|
|
īÓ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
īÓ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ĄĄ
īÓ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·ĻĢŧ
ĄĄ
ÓÉÉÏŋÉÖŠĢšČįđûīÓ![]() ĢŽ
ĢŽ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]()
![]() ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ļöÁŽÐøĩÄŨÔČŧĘýĢŽÓÐ______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ĢĻÎĘĖâ―âūöĢĐČįđûīÓ![]() ĢŽ
ĢŽ![]() ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ
ļöÁŽÐøĩÄŨÔČŧĘýÖÐŅĄÔņ![]() ļöÁŽÐøĩÄŨÔČŧĘý
ļöÁŽÐøĩÄŨÔČŧĘý![]() ĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ĢŽÓÐ_______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ĢĻĘĩžĘÓĶÓÃĢĐÎŌÃĮÔËÓÃÉÏÃæĖ―ūŋĩÃĩ―ĩÄ―áÂÛĢŽŋÉŌÔ―âūöÉúŧîÖÐĩÄŌŧÐĐĘĩžĘÎĘĖâ.
ĢĻ1ĢĐ―ņÄęđúĮėÆßĖėģĪžŲÆÚžäĢŽÐĄÁÁÏëēΞÓÄģÂÃÐÐÉįŨéÖŊĩÄĮāĩšÁ―ČÕÓÎĢŽÔÚģöÐÐČÕÆÚÉÏĢŽËûđēÓÐ______ÖÖēŧÍŽĩÄŅĄÔņ.
ĢĻ2ĢĐÐĮÆÚĖėĢŽÐĄÃũĄĒÐĄĮŋšÍÐĄŧŠČýļöšÃÅóÓŅČĨĩįÓ°ÔšđÛŋīĄķÎŌšÍÎŌĩÄŨæđúĄ·ĢŽĘÛÆąÔąĀî°ĒŌĖΊËûÃĮĖáđĐÁËĩÚÆßÅÅ![]() šÅĩ―
šÅĩ―![]() šÅĩÄĩįÓ°ÆąČÃËûÃĮŅĄÔņĢŽČįđûËûÃĮÏëÄÃČýÕÅÁŽšÅÆąĢŽÔōŌŧđēÓÐ______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
šÅĩÄĩįÓ°ÆąČÃËûÃĮŅĄÔņĢŽČįđûËûÃĮÏëÄÃČýÕÅÁŽšÅÆąĢŽÔōŌŧđēÓÐ______ÖÖēŧÍŽĩÄŅĄÔņ·―·Ļ.
ĢĻÍØÕđŅÓÉėĢĐČįÍžĢŽ―ŦŌŧļö![]() ĩÄÍž°ļ·ÅÖÃÔÚ
ĩÄÍž°ļ·ÅÖÃÔÚ![]() ĩÄ·―ļņÖ―ÖÐĢŽĘđËüĮĄšÃļĮŨĄÆäÖÐĩÄËÄļöÐĄÕý·―ÐÎĢŽđēÓÐ______ÖÖēŧÍŽĩÄ·ÅÖ÷―·Ļ.
ĩÄ·―ļņÖ―ÖÐĢŽĘđËüĮĄšÃļĮŨĄÆäÖÐĩÄËÄļöÐĄÕý·―ÐÎĢŽđēÓÐ______ÖÖēŧÍŽĩÄ·ÅÖ÷―·Ļ.
ĄūĖâÄŋĄŋŌŅÖŠŌŧīΚŊĘýy1Ģ―kx+mĢĻkĄŲ0ĢĐšÍķþīΚŊĘýy2Ģ―ax2+bx+cĢĻaĄŲ0ĢĐĩÄŨÔąäŨîxšÍķÔÓĶšŊĘýÖĩy1ĢŽy2ĩÄēŋ·ÖķÔÓĶÖĩČįąíĢš
x | Ą | Đ1 | 0 | 2 | 4 | Ą |
y1 | Ą | 0 | 1 | 3 | 5 | Ą |
x | Ą | Đ1 | 1 | 3 | 4 | Ą |
y2 | Ą | 0 | Đ4 | 0 | 5 | Ą |
ĩąy1ĄÝy2ĘąĢŽŨÔąäÁŋxĩÄČĄÖĩ·ķÍžĘĮ_____ĢŪ