ЬтФПФкШн
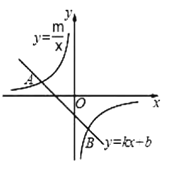
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЕФСНИіЭМаЮMгыNЃЌИјГіШчЯТЖЈвхЃКPЮЊЭМаЮMЩЯШЮвтвЛЕуЃЌQЮЊЭМаЮNЩЯШЮвтвЛЕуЃЌШчЙћPЃЌQСНЕуМфЕФОрРыгазюаЁжЕЃЌФЧУДГЦетИізюаЁжЕЮЊЭМаЮMЃЌNМфЕФЁАКЭФРОрРыЁБЃЌМЧзїdЃЈMЃЌNЃЉЃЎШєЭМаЮMЃЌNгаЙЋЙВЕуЃЌдђdЃЈMЃЌNЃЉЃН0ЃЎ
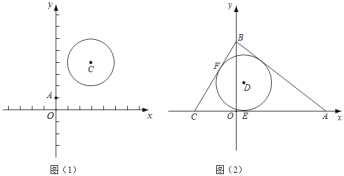
ЃЈ1ЃЉШчЭМЃЌAЃЈ0ЃЌ1ЃЉЃЌCЃЈ3ЃЌ4ЃЉЃЌЁбCЕФАыОЖЮЊ2ЃЌдђdЃЈCЃЌЁбCЃЉЃНЁЁ ЁЁЃЌdЃЈOЃЌЁбCЃЉЃНЁЁ ЁЁЃЛ
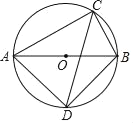
ЃЈ2ЃЉвбжЊЃЌШчЭМЃЌЁїABCЕФвЛБпACдкxжсЩЯЃЌBдкyжсЩЯЃЌЧвACЃН8ЃЌABЃН7ЃЌBCЃН5ЃЎ
ЂйDЪЧЁїABCФквЛЕуЃЌШєACЁЂBCЗжБ№ЧаЁбDгкEЁЂFЃЌЧвdЃЈCЃЌDЃЉЃН2dЃЈDЃЌABЃЉЃЌХаЖЯABгыЁбDЕФЮЛжУЙиЯЕЃЌВЂЧѓГіDЕуЕФзјБъЃЛ
ЂкШєвдrЮЊАыОЖЃЌЂйжаЕФDЮЊдВаФЕФЁбDЃЌгаdЃЈBЃЌЁбDЃЉЃО1ЃЌdЃЈCЃЌЁбDЃЉЃМ2ЃЌжБНгаДГіrЕФШЁжЕЗЖЮЇЁЁ ЁЁЃЎ
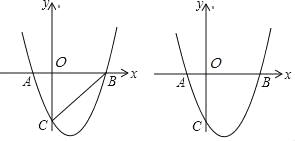
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ3ЃЛЃЈ2ЃЉЂйABЪЧЁбOЕФЧаЯпЃЌЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЭМаЮMЁЂMМфЕФЁАКЭФРОрРыЁБЕФЖЈвхМДПЩЧѓНт;
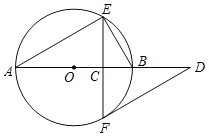
ЃЈ2ЃЉЂйСЌНгDFЃЌDEЃЌзїDHЁЭABгкH. ЩшOCЃНx.ЯШжЄУїЁЯCBOЃН30ЁуЃЌдйжЄУїDH=DEМДПЩНтОіЮЪЬт
ЂкЯШЧѓГіЕуDЕФзјБъЃЌСаГіВЛЕШЪНзщЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉЁпAЃЈ0ЃЌ1ЃЉЃЌCЃЈ3ЃЌ4ЃЉЃЌЁбCЕФАыОЖЮЊ2ЃЌ
ЁрdЃЈCЃЌЁбCЃЉЃН2ЃЌdЃЈOЃЌЁбCЃЉЃНOCЉ2ЃН![]() Љ2ЃН3ЃЌ
Љ2ЃН3ЃЌ
ЙЪД№АИЮЊ2ЃЌ3ЃЎ
ЃЈ2ЃЉЂйСЌНгDFЃЌDEЃЌзїDHЁЭABгкHЃЎЩшOCЃНxЃЎ
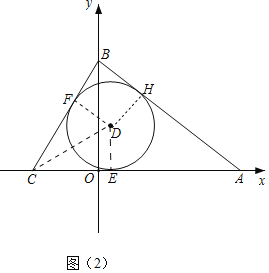
ЁпOB2ЃНBC2ЉOC2ЃНAB2ЉAO2ЃЌ
Ёр52Љx2ЃН72ЉЃЈ8ЉxЃЉ2ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрBCЃН2OCЃЌ
ЁрЁЯCBOЃН30ЁуЃЌЁЯBCOЃН60ЁуЃЌ
ЁпCEЃЌCFЪЧЁбOЕФЧаЯпЃЌ
ЁрCDЦНЗжЁЯBCAЃЌ
ЁрЁЯDCEЃНЁЯDCBЃН30ЁуЃЌ
ЁрDCЃН2DEЃЌ
ЁпdЃЈCЃЌDЃЉЃН2dЃЈDЃЌABЃЉЃЌ
ЁрCDЃН2DHЃЌ
ЁрDHЃНDEЃЌ
ЁрABЪЧЁбOЕФЧаЯпЃЎ
ЂкгЩЂйПЩжЊOBЃН![]() OCЃН
OCЃН![]() ЃЌЩшDFЃНDEЃНDHЃНxЃЌ
ЃЌЩшDFЃНDEЃНDHЃНxЃЌ
ЁпSЁїABCЃН![]() ACOCЃН
ACOCЃН![]() ЃЈAC+BC+ABЃЉxЃЌ
ЃЈAC+BC+ABЃЉxЃЌ
ЁрxЃН![]() ЃЌ
ЃЌ
ЁрCEЃН![]() DEЃН3ЃЌCDЃН2DEЃН2
DEЃН3ЃЌCDЃН2DEЃН2![]() ЃЌ
ЃЌ
ЁрOEЃН3Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁпBЃЈ0ЃЌ
ЃЉЃЌЁпBЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрBDЃН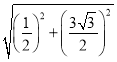 ЃН
ЃН![]() ЃЌ
ЃЌ
гЩЬтвтЃК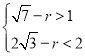 ЃЌ
ЃЌ
НтЕУ2![]() Љ2ЃМrЃМ
Љ2ЃМrЃМ![]() Љ1ЃЎ
Љ1ЃЎ
ЙЪД№АИЮЊ2![]() Љ2ЃМrЃМ
Љ2ЃМrЃМ![]() Љ1ЃЎ
Љ1ЃЎ

 ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ