题目内容
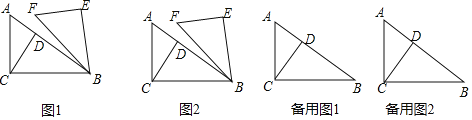
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点D,将
于点D,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 得到
得到![]()
![]() 如图2,当
如图2,当![]() 时,求点C、E之间的距离;
时,求点C、E之间的距离;
![]() 在旋转过程中,当点A、E、F三点共线时,求AF的长;
在旋转过程中,当点A、E、F三点共线时,求AF的长;
![]() 连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
【答案】(1)CE=![]() ;(2)AF的长为
;(2)AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() ;(3)CP的最小值=OC﹣OP=2﹣
;(3)CP的最小值=OC﹣OP=2﹣![]() .
.
【解析】
(1)只要证明∠CBE=90°,求出BE,BC利用勾股定理即可解决问题.
(2)分两种情形画出图形分别求解即可.
(3)如图3中,取AB的中点O,连接OP,CO.利用三角形的中位线定理可得OP=![]() ,推出点P的运动轨迹是以O为圆心
,推出点P的运动轨迹是以O为圆心![]() 为半径的圆,由此即可解决问题.
为半径的圆,由此即可解决问题.
解:(1)如图1中,
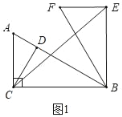
在Rt△ABC中,∵∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,BC=![]() =2
=2![]() ,
,
∵CD⊥AB,
∴![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=![]() =
=![]() =
=![]() ,
,
∴BD=BE=![]() =3,
=3,
∵∠ABE=α=60°,
∴∠CBE=30°+60°=90°,
∴CE=![]() =
=![]() =
=![]() .
.
(2span>)如图2﹣1中,

∵A,F,E三点共线,
∴∠AEB=90°,AE=![]() =
=![]() =
=![]() ,
,
∴AF=AE﹣EF=![]() ﹣
﹣![]() .
.
如图2﹣2中,
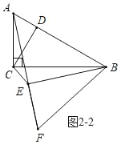
当A,E,F共线时,∠AEB=90°,AE=![]() =
=![]() =
=![]() ,
,
∴AF=AE+EF=![]() +
+![]() .
.
综上所述,AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() .
.
(3)如图3中,取AB的中点O,连接OP,CO.

∵AO=OB,AP=PF,
∴OP=![]() BF=
BF=![]() BC=
BC=![]() ,
,
∴点P的运动轨迹是以O为圆心![]() 为半径的圆,
为半径的圆,
∵OC=![]() AB=2,
AB=2,
∴CP的最小值=OC﹣OP=2﹣![]() .
.
故答案为:(1)CE=![]() ;(2)AF的长为
;(2)AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() ;(3)CP的最小值=OC﹣OP=2﹣
;(3)CP的最小值=OC﹣OP=2﹣![]() .
.

练习册系列答案
相关题目