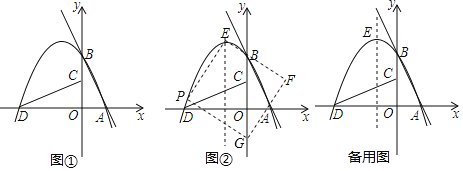
��Ŀ����
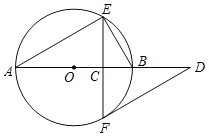
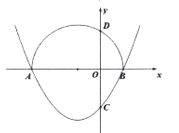
����Ŀ����ͼ�٣���ֱ��l�Uy=��2x+4��x���ڵ�A����y���ڵ�B������AOB�Ƶ�O��ʱ����ת![]() �õ���COD������A��B��D��������h�Uy=ax2+bx+4��
�õ���COD������A��B��D��������h�Uy=ax2+bx+4��
��1����������h�ı���ʽ��
��2������y��ƽ�е�ֱ��m��1����һ����λ�����ٶȴ�y������ƽ�ƣ����߶�CD�ڵ�M����������h�ڵ�N�����߶�MN�����ֵ��
��3����ͼ�ڣ���EΪ������h�Ķ��㣬��P��������h�ڵڶ�������һ���㣨�����D��B�غϣ�������PE����PEΪ����ͼʾһ���������PEFG�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣬������F��Gǡ������y����ʱ��ֱ��д����Ӧ�ĵ�P�����꣮
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��![]() ��
��![]()
��������
��1������ֱ��l�Ľ���ʽ�õ�A,B��������꣬�ٸ�����ת�õ�D������꣬Ȼ�����ô���ϵ�����������ߵĽ���ʽ����.
��2�������N�����꣬�������ú������ʾ������ͬʱҲ���Ա�ʾ��M�����꣬��MN�ij��Ⱦ���N����M���������֮�����֮������һ������N�������Ķ��κ��������ö��κ�������ֵ����.
��3���ֱ�Զ���F�Ͷ���G��y���Ϸ�������ۣ������P�����꼴��
��1����ֱ��l��![]() ��x���ڵ�A����y���ڵ�B��
��x���ڵ�A����y���ڵ�B��
��![]() ��
��![]() .
.
����![]() �Ƶ�O��ʱ����ת
�Ƶ�O��ʱ����ת![]() �õ�
�õ�![]() ��
��
��![]() ��
��![]() .
.
�����A��B��D��������h�Ľ���ʽΪ��![]() .
.
��B���������ɵã�![]() ��
��
��![]() ����������h�Ľ���ʽΪ
����������h�Ľ���ʽΪ![]() ��
��
��2����![]() ��
��![]() ��
��
��ֱ��CD�Ľ���ʽΪ![]() .
.
��N������Ϊ![]() ����M������Ϊ
����M������Ϊ![]() .
.
��![]() ��
��
����![]() ʱ��MN������ֵΪ
ʱ��MN������ֵΪ![]() ��
��
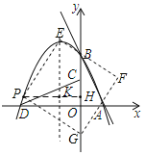
��3����G���� y���ϣ���ͼ����PH��y����H���������߶Գ�����K��
��![]() ��
��![]()
![]() �У�
��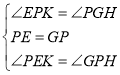 ��
�� ![]()
��![]() ��
��![]() .
.
��![]() ����
����![]() .
.
��![]() ��
��
��![]() ,
,![]() .
.
��![]() ������
������![]() .
.
���P���������![]() ��
��![]() .
.
��F���� y���ϣ���ͼ����PR��ֱ�����߶Գ�����R��FQ��ֱ�����߶Գ�����Q����![]() PER��
PER��![]() EFQ����ER=FQ��
EFQ����ER=FQ��
���ԣ�![]() �����У�
������![]()
��![]() ��
��![]() ����ȥ��
����ȥ��

��P���������![]() .
.
��������������Ҫ���P����������������ֱ�Ϊ��
![]() ��
��![]() ��
��![]() ��
��