题目内容
【题目】定义:连结菱形的一边中点与对边的两端点的线段把它分成三个三角形,如果其中有两个三角形相似,那么称这样的菱形为自相似菱形.
(1)判断下列命题是真命题,还是假命题?
①正方形是自相似菱形;
②有一个内角为60°的菱形是自相似菱形.
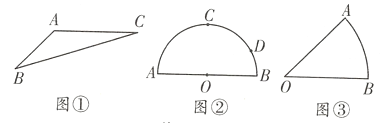
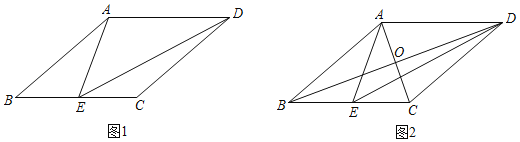
③如图1,若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED.
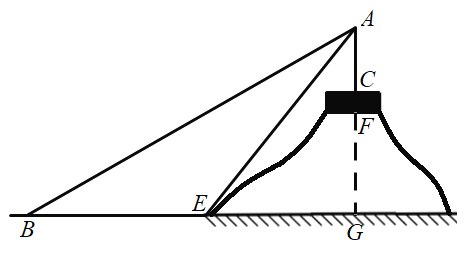
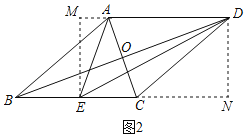
(2)如图2,菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点.
①求AE,DE的长;
②AC,BD交于点O,求tan∠DBC的值.
【答案】(1)见解析;(2)①AE=2![]() ,DE=4
,DE=4![]() ;②tan∠DBC=
;②tan∠DBC=![]() .
.
【解析】
(1)①证明△ABE≌△DCE(SAS),得出△ABE∽△DCE即可;
②连接AC,由自相似菱形的定义即可得出结论;
③由自相似菱形的性质即可得出结论;
(2)①由(1)③得△ABE∽△DEA,得出![]() ,求出AE=2
,求出AE=2![]() ,DE=4
,DE=4![]() 即可;
即可;
②过E作EM⊥AD于M,过D作DN⊥BC于N,则四边形DMEN是矩形,得出DN=EM,DM=EN,∠M=∠N=90°,设AM=x,则EN=DM=x+4,由勾股定理得出方程,解方程求出AM=1,EN=DM=5,由勾股定理得出DN=EM=![]() =
=![]() ,求出BN=7,再由三角函数定义即可得出答案.
,求出BN=7,再由三角函数定义即可得出答案.
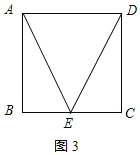
解:(1)①正方形是自相似菱形,是真命题;理由如下:
如图3所示:
∵四边形ABCD是正方形,点E是BC的中点,
∴AB=CD,BE=CE,∠ABE=∠DCE=90°,
在△ABE和△DCE中
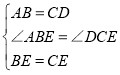 ,
,
∴△ABE≌△DCE(SAS),
∴△ABE∽△DCE,
∴正方形是自相似菱形,
故答案为:真命题;
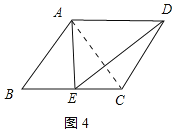
②有一个内角为60°的菱形是自相似菱形,是假命题;理由如下:
如图4所示:
连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD,AD∥BC,AB∥CD,
∵∠B=60°,
∴△ABC是等边三角形,∠DCE=120°,
∵点E是BC的中点,
∴AE⊥BC,
∴∠AEB=∠DAE=90°,
∴只能△AEB与△DAE相似,
∵AB∥CD,
∴只能∠B=∠AED,
若∠AED=∠B=60°,则∠CED=180°﹣90°﹣60°=30°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠CED=∠CDE,
∴CD=CE,不成立,
∴有一个内角为60°的菱形不是自相似菱形,
故答案为:假命题;
③若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,
则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED,是真命题;理由如下:
∵∠ABC=α(0°<α<90°),
∴∠C>90°,且∠ABC+∠C=180°,△ABE与△EDC不能相似,
同理△AED与△EDC也不能相似,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠AEB=∠DAE,
当∠AED=∠B时,△ABE∽△DEA,
∴若菱形ABCD是自相似菱形,∠ABC=α(0°<α<90°),E为BC中点,
则在△ABE,△AED,△EDC中,相似的三角形只有△ABE与△AED,
故答案为:真命题;
(2)①∵菱形ABCD是自相似菱形,∠ABC是锐角,边长为4,E为BC中点,
∴BE=2,AB=AD=4,
由(1)③得:△ABE∽△DEA,
∴![]()
∴AE2=BEAD=2×4=8,
∴AE=2![]() ,DE=
,DE=![]() =
=![]() =4
=4![]() ,
,
故答案为:AE=2![]() ;DE=4
;DE=4![]() ;
;
②过E作EM⊥AD于M,过D作DN⊥BC于N,如图2所示:则四边形DMEN是矩形,
∴DN=EM,DM=EN,∠M=∠N=90°,
设AM=x,则EN=DM=x+4,
由勾股定理得:EM2=DE2﹣DM2=AE2﹣AM2,
即(4![]() )2﹣(x+4)2=(2
)2﹣(x+4)2=(2![]() )2﹣x2,
)2﹣x2,
解得:x=1,
∴AM=1,EN=DM=5,
∴DN=EM=![]() =
=![]() ,
,
在Rt△BDN中,
∵BN=BE+EN=2+5=7,
∴tan∠DBC=![]() ,
,
故答案为:![]() .
.

 名校课堂系列答案
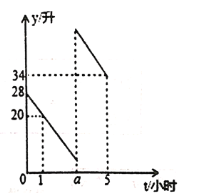
名校课堂系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?