题目内容
【题目】问题提出
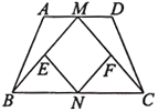
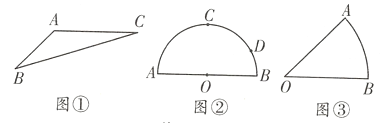
（1）如图①，在
中，
，求的面积．
问题探究
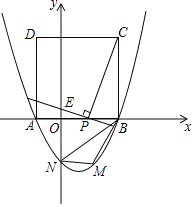
（2）如图②，半圆
的直径
，
是半圆
的中点，点
在
上，且
，点
是
上的动点，试求
的最小值．
问题解决
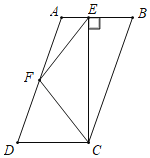
（3）如图③，扇形
的半径为
在选点，在边
上选点
，在边
上选点
，求
的长度的最小值．
【答案】（1）12；（2）
；（3）
．
【解析】
（1）如图1中，过点
作
，交
延长线于点
，通过构造直角三角形，求出BD利用三角形面积公式求解即可.
（2）如图示，作点关于
的对称点
，交于点
，连接
，交于点
，连接
、
、
，过点作
，交
延长线于点
，确定点P的位置，利用勾股定理与矩形的性质求出CQ的长度即为答案.
（3）解图3所示，在
上这一点作点关于
的对称点
，作点关于
的对称点
，连接
，交于点
，交于点
，连接
，通过轴对称性质的转化，最终确定最小值转化为SN的长.
（1）如解图1所示，过点作，交延长线于点，
，
，
，交延长线于点，
为等腰直角三角形，且
，
，
在
中，
，
，即
，
，
，解得：
，
，
．
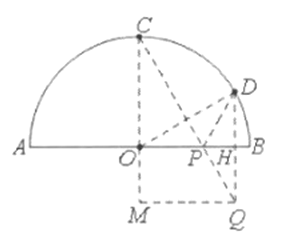
（2）如解图2所示，作点关于的对称点，交于点，连接，交于点，连接、、，过点作，交延长线于点，
关于的对称点，交于点，
，
，
点为上的动点，
，
当点处于解图2中的位置，
取最小值，且最小值为的长度，
点
为半圆的中点，
，
，
，
，
，
在
中，由作图知，
，且
，
，
，
由作图知，四边形
为矩形，
，
，
，
的最小值为．
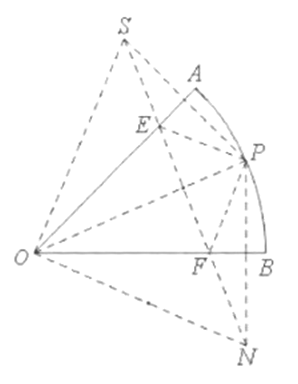
（3）如解图3所示，在上这一点作点关于的对称点，作点关于的对称点，连接，交于点，交于点，连接，
点关于的对称点，点关于的对称点，连接，交于点，交于点，
，
，
，
，
．
，
，
为上的点，为上的点
，
当点
处于解图3的位置时，
的长度取最小值，最小值为的长度，
，
，
．
扇形
的半径为
，
，
在
中，
，
的长度的最小值为．
练习册系列答案
相关题目
