题目内容
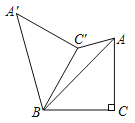
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝BC＝2；若将△ABC绕点B逆时针旋转60°到△A′BC′的位置，连接C′A，则C′A的长为（ ）
A.
B.
C.
D.2﹣
【答案】B
【解析】
连接AA′，延长AC′交BA′于点M，证明△AA′M为直角三角形，在Rt△AA′M根据勾股定理可求得AM，在等腰直角三角形A′BC′中根据斜边的中线等于斜边的一半求得MC′，于是AC′可求.
解：如图，连接AA′，延长AC′交BA′于点M，
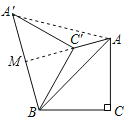
由题意得：∠ABA′＝60°，BA＝B′A，
∴△BAA′为等边三角形，
∴∠BAA′＝60°，AB＝A′A；
在△BAC′与△A′AC′中，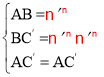
，
∴△BAC′≌△A′AC′（SSS），
∴∠MAA′＝∠MAB＝30°，
∴AM⊥BA′，且BM＝A′M；
由题意得：AB2＝22+22＝8，
∴AA′=A′B＝AB＝2
，A′M＝，
∴C′M＝
A′B＝；由勾股定理可求：AM＝
，
∴C′A＝﹣，
故选：B．
练习册系列答案
相关题目
