题目内容
【题目】我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理．如图，若a＝4，b＝6，则该直角三角形的周长为（ ）
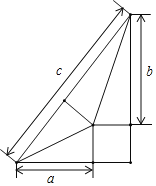
A.18B.20C.24D.26
【答案】C
【解析】
设小正方形的边长为x，根据已知条件得到AB=4+6=10，根据勾股定理列方程求得x=1，x=-6（不合题意舍去），根据三角形的周长公式即可得到结论．
解:设小正方形的边长为x，
∵a＝4，b＝6，
∴AB＝4+6＝10，
在Rt△ABC中，AC2+BC2＝AB2，
即（4+x）2+（6+x）2＝102，
解得：x＝2，x＝﹣12（不合题意舍去），
∴该直角三角形的周长为：4+2+6+2+10＝24．
故选：C．
练习册系列答案
相关题目
