��Ŀ����
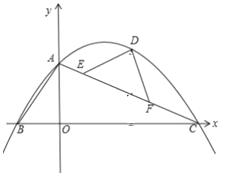
����Ŀ����ͼ��ijУ��ѧ¥AB�ĺ�����һ������CD�������������ļн���22ʱ��
��ѧ¥�ڽ������ǽ�����¸�2m��Ӱ��CE���������������ļн���45ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��13m�ľ���(B��F��C��һ��ֱ����)��
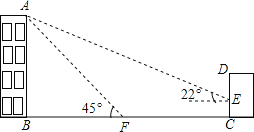
(1)���ѧ¥AB�ĸ߶ȣ�
(2)ѧУҪ��A��E֮���һЩ���죬�������A��E֮��ľ���(�����������)��
(�ο����ݣ�sin22��![]() ��cos22��
��cos22��![]() ��tan22��
��tan22��![]() )
)
���𰸡���1��12m��2��27m
��������
��1�����ȹ���ֱ����������AEM������![]() ��������ɡ�
��������ɡ�
��2������Rt��AME�У�![]() �����AE���ɡ�
�����AE���ɡ�
�⣺��1������E��EM��AB������ΪM��
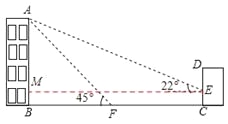
��ABΪx��
��Rt��ABF����AFB=45����
��BF=AB=x��
��BC=BF��FC=x��13��
��Rt��AEM����AEM=22����AM=AB��BM=AB��CE=x��2��
����![]() ����
����![]() ����ã�x��12��
����ã�x��12��
����ѧ¥�ĸ�12m��
��2���ɣ�1���ɵ�ME=BC=x+13��12+13=25��
��Rt��AME��![]() ��
��
��AE=MEcos22���![]() ��
��
��A��E֮��ľ���ԼΪ27m��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ