题目内容
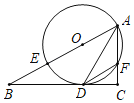
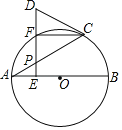
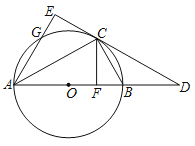
【题目】已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,交⊙O于G,CF⊥AB于F,点C是弧BG的中点.
(1)求证:DE是⊙O的切线;
(2)若AF,BF(AF>BF)是一元二次方程x2﹣8x+12=0的两根,求CE和AG的长.
【答案】(1)见解析;(2)2![]() ,4
,4
【解析】
(1)连接OC,求出AC平分∠EAF,推出OC∥AE,推出OC⊥DE,根据切线判定推出即可;
(2)连接CG,得到CG=BC,解方程求得AF=6,BF=2,得到AB=8,根据射影定理得到AC=4![]() ,BC=4,解直角三角形即可得到结论.
,BC=4,解直角三角形即可得到结论.
(1)证明:连接OC,
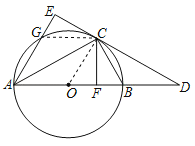
∵点C是弧BG的中点,
![]()
∴∠EAC=∠CAF,
∵OA=OC,
∴∠CAF=∠OCA,
∴∠OCA=∠EAC,
∴OC∥AE,
∵AE⊥DE,
∴OC⊥DE,
∵OC为⊙O半径,
∴DE是⊙O的切线;
(2)连接CG,
![]()
∴CG=BC,
∵AF,BF(AF>BF)是一元二次方程x2﹣8x+12=0的两根,x2﹣8x+12=0的两根为![]() ,
,
∴AF=6,BF=2,
∴AB=8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CF⊥AB,
∴AC2=AFAB=6×8=48,BC2=BFAB=16,
∴AC=4![]() ,BC=4,
,BC=4,
∴tan∠CAB=![]() =
=![]() ,
,
∴∠CAE=∠CAB=30°,
∴CE=![]() AC=2
AC=2![]() ,AE=
,AE=![]() AC=6,
AC=6,
∵CG=BC=4,
∴EG=![]() =
=![]() =2,
=2,
∴AG=4.

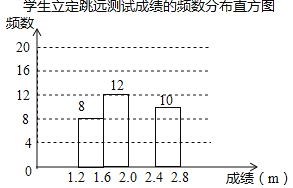
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?