题目内容
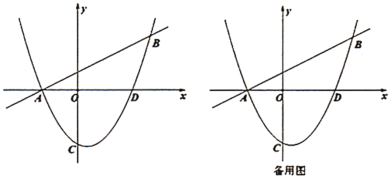
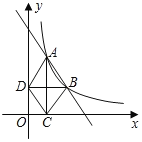
【题目】如图,已知二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,其中
,其中![]() .
.
(1)求点![]() 的坐标,并用含
的坐标,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)连接![]() ,
,![]() ,当
,当![]() 为锐角时,求
为锐角时,求![]() 的取值范围;
的取值范围;
(3)若![]() 为
为![]() 轴上一个动点,连接
轴上一个动点,连接![]() ,当点
,当点![]() 的坐标为
的坐标为![]() 时,直接写出
时,直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() 的坐标为
的坐标为![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由函数解析式可知对称轴为直线![]() ,又因为A、B两点是抛物线与x轴的交点,两点关于对称轴对称,可得点
,又因为A、B两点是抛物线与x轴的交点,两点关于对称轴对称,可得点![]() 的坐标为
的坐标为![]() ,将A点坐标代入函数解析式可得k的表达式.
,将A点坐标代入函数解析式可得k的表达式.
(2)当![]() 时,
时,![]() ,利用相似三角形的性质求得
,利用相似三角形的性质求得![]() ,由(1)得
,由(1)得![]() ,即
,即![]() ,所以当
,所以当![]() 为锐角时
为锐角时![]() .
.
(3)在![]() 中,
中,![]() ,可得
,可得![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,则
,则![]() ,
,![]() ,即
,即![]() 的最小值为点
的最小值为点![]() 到
到![]() 的距离,求得AH的值即可.
的距离,求得AH的值即可.
解:(1)![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() ,
,
又该函数图象过点![]() .
.
∴由对称性可知点![]() 的坐标为
的坐标为![]() .
.
把![]() ,
,![]() 代入,得
代入,得![]() ,故
,故![]() .
.
(2)当![]() 时,
时,![]() ,
,
于是![]() ,
,
![]() ,即
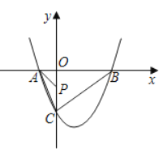
,即![]() ,如图1,
,如图1,
∴由(1)得![]() ,即
,即![]() .
.
![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() .
.
解:在![]() 中,
中,![]() ,
,
![]() .
.
作![]() ,垂足为点
,垂足为点![]() ,则
,则![]() ,
,
![]() ,
,
即![]() 的最小值为点
的最小值为点![]() 到
到![]() 的距离
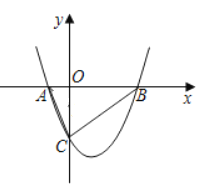
的距离![]() ,如图2,
,如图2,
![]() .
.

练习册系列答案
相关题目