题目内容
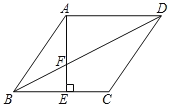
【题目】如图,在正方形![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,高
边上,高![]() 与正方形的边长相等,连接
与正方形的边长相等,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法:①
,下列说法:①![]() ;②连接
;②连接![]() ,
,![]() ,则
,则![]() 为直角三角形;③
为直角三角形;③![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() 的长为
的长为![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
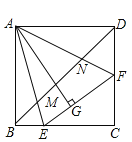
A.4B.3C.2D.1
【答案】A
【解析】
根据正方形的性质及HL定理求得Rt△AEB≌Rt△AEG,Rt△AFD≌Rt△AFG,从而求得∠EAB=∠EAG,∠FAD=∠FAG,然后求得2∠EAG+2∠FAG=90°,从而得到![]() ,由此判断①;
,由此判断①;
将△ADN绕点A顺时针旋转90°至△ABH位置,连接MH,MG,NG,由旋转的性质根据结合SAS定理求得△AHM≌△ANM,得到MN=MH,结合正方形和旋转的性质求得∠HBM=∠ABH+∠ABD=90°,从而可得MH2=HB2+BM2,然后根据SAS定理求得△ABM≌△AGM,△AND≌△AANG,从而得到BM=GM,DN=GN,从而求得MN2=MG2+NG2,由此判断②;
由垂直可得∠AEG =90°-∠EAG,然后结合①中已证∠EAG+∠FAG=∠EAG+∠FAD=45°,可得∠ANM=90°-∠EAG,由此得到∠AEG =∠ANM,然后根据AA定理求得三角形形式,由此判断③;
旋转△ABE到△ADH,由旋转性质和SAS定理可得得△ABE≌△ADH,△AEF≌△AHF,设CF=a,在Rt△CEF中,根据勾股定理列方程求a,从而求得正方形的边长,设MN=x,结合②中的结论列方程求x的值,从而判断④.
解:如图中,
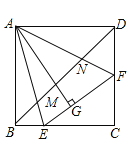
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∵AG⊥EF,
∴∠AGE=∠ABC=90°,
在Rt△AEB和Rt△AEG中,![]() ,
,
∴Rt△AEB≌Rt△AEG,
∴∠EAB=∠EAG,
同理可证Rt△AFD≌Rt△AFG,
∴∠FAD=∠FAG,
∴2∠EAG+2∠FAG=90°,
∴∠EAG+∠FAG=45°,
∴∠EAF=45°,故①正确;
如图②,将△ADN绕点A顺时针旋转90°至△ABH位置,连接MH,MG,NG
由旋转知:∠BAH=∠DAN,AH=AN,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠HAM=∠BAM+∠BAH=45°,
∴∠HAM=∠NAM,又AM=AM,
∴△AHM≌△ANM,
∴MN=MH
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°.
由旋转知:∠ABH=∠ADB=45°,HB=ND,
∴∠HBM=∠ABH+∠ABD=90°,
∴MH2=HB2+BM2,
∴MN2=MB2+ND2.
又∵AB=AG,∠EAB=∠EAG,AM=AM
∴△ABM≌△AGM
∴BM=GM
同理可证:△AND≌△AANG
∴DN=GN
∴MN2=MG2+NG2
即![]() 为直角三角形,故②正确;
为直角三角形,故②正确;
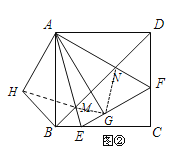
∵AG⊥EF
∴∠AEG =90°-∠EAG
又∵∠ANM=∠BDA+∠DAF=45°+∠DAF
由①可知:∠EAG+∠FAG=∠EAG+∠FAD=45°
∴∠ANM=90°-∠EAG
∴∠AEG =∠ANM
又∵![]()
∴![]() ,故③正确;
,故③正确;
如图3中,
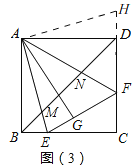
旋转△ABE到△ADH,△ABE≌△ADH
∴DH=BE=2,
同理②中可证:△AEF≌△AHF,
∴FH=EF,设CF=a
∴CD=CF+DF=a+3,EF=FH=DF+DH=5,
∵四边形ABCD是正方形,
∴BC=CD=a+3
∴CE=BC-BE=a+3-2=a+1,
在Rt△CEF中,根据勾股定理得,(a+1)2+32=25
∴a=3或a=-5(舍),
∴CF=3,
∴CD=6,
∴正方形的边长为6;
由正方形ABCD的边长为6,
∴BD=![]() CD=6
CD=6![]() ,
,

由①可知△MAN=45°,
∵AB=AD,∠BAD=90°,
由②得BM2+DN2=MN2,
设MN=x,
∵BD=6![]() ,BM=
,BM=![]() ,
,
∴DN=![]()
∴![]()
解得x=![]() ,
,
∴MN=![]() ,故④正确
,故④正确
故选:A.

【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |
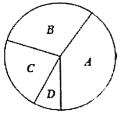
(1)表中![]() __________;
__________;![]()
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)