题目内容
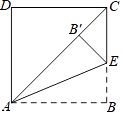
【题目】如图，在边长为2的正六边形ABCDEF中，点P是其对角线BE上一动点，连接PC、PD，则△PCD的周长的最小值是 ．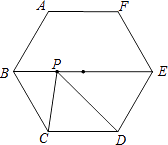 
【答案】6
【解析】解：要使△PCD的周长的最小，即PC+PD最小．
利用正多边形的性质可得点C关于BE的对称点为点A，连接AD交BE于点P'，那么有P'C=P'A，P'C+P'D=AD最小．
又易知ABCD为等腰梯形，∠BAD=∠CDA=60°，
则作BM⊥AD于点M，CN⊥AD于点N，
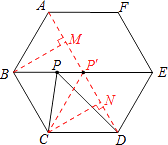
∵AB=2，
∴AM= 
AB=1，
∴AM=DN=1，从而AD=4，
故△PCD的周长的最小值为6．
所以答案是：6．
【考点精析】本题主要考查了轴对称-最短路线问题的相关知识点，需要掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径才能正确解答此题．
练习册系列答案
名校课堂系列答案
相关题目
