题目内容
【题目】如图,将正方形ABCD的边AB沿AE折叠,使点B落在对角线AC上,则∠BAE的度数为 . 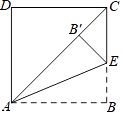
【答案】22.5°
【解析】解:∵四边形ABCD为正方形,
∴∠BAC=45°.
由折叠的性质可知:∠BAE=∠B′AE,
∴∠BAE= ![]() ∠BAC=22.5°.
∠BAC=22.5°.
所以答案是:22.5°.
【考点精析】利用正方形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目