题目内容
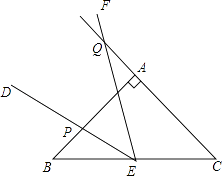
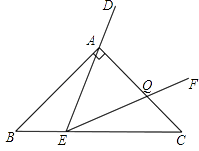
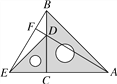
【题目】把两个含有45°角的直角三角板ACB和DEC如图放置,点A,C,E在同一直线上,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
(1)求证:△ADC≌△BEC;
(2)猜想AD与EB是否垂直?并说明理由.
【答案】(1)证明见解析;(2)AD⊥EB.理由见解析.
【解析】(1)由SAS判定△ADC≌△BEC;
(2)根据全等三角形的性质可知:对应边相等AD=BE、对应角相等∠BEC=∠ADC;加上已知条件来求∠AFE=90°即可.
(1)∵△ABC和△ECD都是等腰直角三角形,∴∠ECD=∠BCA=90°,CE=CD,BC=AC,在△DCA和△ECB中,∵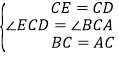 ,∴△ADC≌△BEC(SAS);
,∴△ADC≌△BEC(SAS);
(2)∵△ADC≌△BEC,∴AD=BE,∠BEC=∠ADC,又∠ADC+∠DAC=90°,∴∠BEC+∠DAC=90°,∴∠AFE=90°,即AD⊥BE.

练习册系列答案
相关题目