题目内容
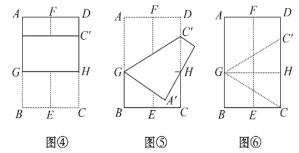
【题目】如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③),沿GH折叠,使点C落在DH上的C′处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′=______度;
(2)图⑥中的△GCC′是_______三角形.

【答案】60, 等边
【解析】
(1)由折叠的性质知:B′C=BC,然后在Rt△B′EC中,含30°角的直角三角形的性质,即可求得∠BCB′的度数;
(2)首先根据题意得:GC平分∠BCB′,即可求得∠GCC′的度数,然后由折叠的性质知:GH是线段CC′的对称轴,可得GC′=GC,即可得△GCC′是等边三角形.
(1)由折叠的性质知:B′C=BC.在Rt△B′EC中,∵EC是斜边B′C的一半,∴∠EB′C=30°,∴∠BCB′=60°,即∠BCB′=60°;
(2)图⑥中的△CGC'是等边三角形.理由如下:
∵GC平分∠BCB′,∴∠GCB=![]() ∠GCC′=
∠GCC′=![]() ∠BCB′=30°,∴∠GCC′=∠BCD﹣∠BCG=60°,由折叠的性质知:GH是线段CC′的对称轴,∴GC′=GC,∴△GCC′是等边三角形.
∠BCB′=30°,∴∠GCC′=∠BCD﹣∠BCG=60°,由折叠的性质知:GH是线段CC′的对称轴,∴GC′=GC,∴△GCC′是等边三角形.

练习册系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从表可知,
①抛物线与x轴的交点为;
②抛物线的对称轴是;
③函数y=ax2+bx+c的最大值为;
④x , y随x增大而增大.