题目内容
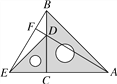
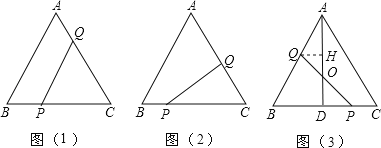
【题目】如图1，在等腰直角△ABC中，∠BAC=90°，AB=AC=2，点E是BC边上一点，∠DEF=45°且角的两边分别与边AB，射线CA交于点P，Q．
（1）如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q．设BP为x，CQ为y，试求y与x的函数关系式，并写出自变量x的取值范围；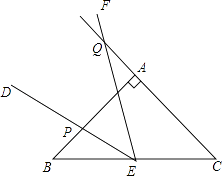
（2）如图3，点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．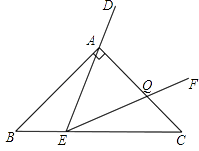
【答案】
（1）
解：∵∠BAC=90°，AB=AC=2，
∴∠B=∠C， 
．
又∵∠FEB=∠FED+∠DEB=∠EQC+∠C，∠DEF=∠C，
∴∠DEB=∠EQC，
∴△BPE∽△CEQ，
∴ 
．
设BP为x，CQ为y，
∴ 
．
∴ 
，自变量x的取值范围是0＜x＜1
（2）
解：∵∠AEF=∠B=∠C，且∠AQE＞∠C，
∴∠AQE＞∠AEF．
∴AE≠AQ．
当AE=EQ时，
∴∠EAQ=∠EQA，
∵∠AEQ=45°，
∴∠EAQ=∠EQA=67.5°，
∵∠BAC=90°，∠C=45，
∴∠BAE=∠QEC=22.5°．
∵在△ABE和△ECQ中，
，
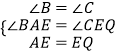∴△ABE≌ECQ（AAS）．
∴CE=AB=2．
∴BE=BC﹣EC= 
；
当AQ=EQ时，可知∠QAE=∠QEA=45°，
∴AE⊥BC．
∴点E是BC的中点．
∴BE= 
．
综上，在∠DEF运动过程中，△AEQ能成等腰三角形，此时BE的长为 或
【解析】（1）根据条件由勾股定理可以求出BC的值，再求出∠DEB=∠EQC，就可以得出△BPE∽△CEQ，由相似三角形的性质就可以得出结论；（2）由∠AEF=∠B=∠C，且∠AQE＞∠C可以得出∠AQE＞∠AEF．从而有AE≠AQ，再分类讨论，当AE=EQ时和AQ=EQ时根据等腰三角形的性质和全等三角形的性质就可以求出BE的值．
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识，掌握全等三角形的对应边相等; 全等三角形的对应角相等，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
