题目内容
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)用五点法画出此函数图象的示意图. 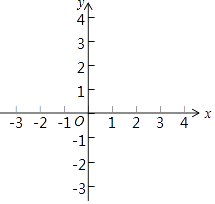
【答案】
(1)解:把(﹣1,﹣8),(0,﹣3)代入y=﹣x2+bx+c得: ![]() ,
,
解得: ![]() ,
,
∴二次函数的表达式为:y=﹣x2+4x﹣3,
y=﹣x2+4x﹣3=﹣(x﹣2)2+1
(2)解:顶点(2,1),
当y=0时,﹣x2+4x﹣3=0,
x2﹣4x+3=0,
(x﹣1)(x﹣3)=0,
x1=1,x2=3,
∴与x轴交点为(1,0)、(3,0),
列表如下:
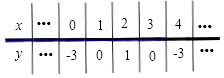
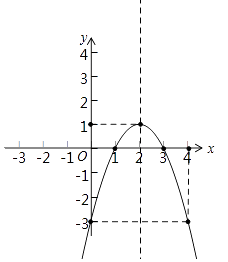
【解析】(1)把已知两点(﹣1,﹣8),(0,﹣3)代入二次函数的解析式求出b和c的值,再配方成顶点式;(2)写出顶点坐标,计算其与x轴的交点和与y轴的交点,列表、描点,画出图象.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从表可知,
①抛物线与x轴的交点为;
②抛物线的对称轴是;
③函数y=ax2+bx+c的最大值为;
④x , y随x增大而增大.