题目内容
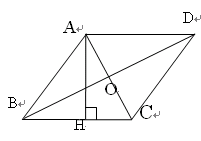
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.

小题1:求证:EB=GD;
小题2:判断EB与GD的位置关系,并说明理由;
小题3:若AB=2,AG= ,求EB的长
,求EB的长

小题1:求证:EB=GD;
小题2:判断EB与GD的位置关系,并说明理由;
小题3:若AB=2,AG=
 ,求EB的长
,求EB的长小题1:见解析
小题2:EB⊥GD理由见解析
小题3:
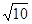
(1)证明:∵四边形ABCD和四边形AEFG都是正方形,
∴AG=AE,AB=AD,∠GAE=∠BAD=90°………………………………….1分
在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∴△GAD≌△EAB……………………………………………………………..2分
∴EB=GD;……………………………………………………………………..3分
(2)EB⊥GD………………………………………………………………………….4分
理由如下:连接BD,
由(1)得:∠ADG=∠ABE,………………………………………………….5分
则在△BDH中,
∠DHB=180°-(∠HDB+∠HBD)
=180°-90°=90°,
∴EB⊥GD……………………………………………………………………….6分
(3)设BD与AC交于点O,
∵AB=AD=2
∴在Rt△ABD中,DB=,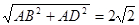
∴OD=OA=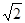 ,………………………………………………………………7分
,………………………………………………………………7分
∴OG=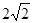 ……………………………………………………………………..8分
……………………………………………………………………..8分
∴EB="GD="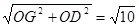
∴AG=AE,AB=AD,∠GAE=∠BAD=90°………………………………….1分
在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
∴△GAD≌△EAB……………………………………………………………..2分
∴EB=GD;……………………………………………………………………..3分
(2)EB⊥GD………………………………………………………………………….4分
理由如下:连接BD,
由(1)得:∠ADG=∠ABE,………………………………………………….5分
则在△BDH中,
∠DHB=180°-(∠HDB+∠HBD)
=180°-90°=90°,
∴EB⊥GD……………………………………………………………………….6分
(3)设BD与AC交于点O,
∵AB=AD=2
∴在Rt△ABD中,DB=,
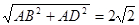
∴OD=OA=
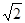 ,………………………………………………………………7分
,………………………………………………………………7分∴OG=
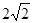 ……………………………………………………………………..8分
……………………………………………………………………..8分∴EB="GD="
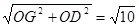

练习册系列答案
相关题目

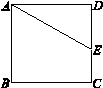




 ,则下底BC的长为 .
,则下底BC的长为 .