题目内容
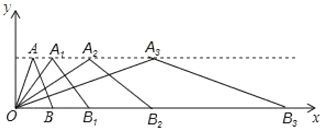
【题目】如图,在平面直角坐标系中,第一次将三角形![]() 变换成三角形
变换成三角形![]() ,第二次将三角形
,第二次将三角形![]() 变换成三角形
变换成三角形![]() ,第三次将三角形变换成三角形
,第三次将三角形变换成三角形![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)观察每次变换前后的三角形,找出规律,按这些变换规律将三角形![]() 变换成三角形
变换成三角形![]() ,求
,求![]() 和
和![]() 的坐标;
的坐标;
(2)若按第(1)题的规律将三角形![]() 进行了
进行了![]() 次变换,得到三角形
次变换,得到三角形![]() ,请推测
,请推测![]() 和
和![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]()
【解析】
(1)据图形,A4的横坐标是A3的横坐标的2倍,纵坐标相同,B4横坐标是B3的2倍,纵坐标是0;
(2)由(1)知An的纵坐标总为3,横坐标为2n,Bn的纵坐标总为0,横坐标为2n+1,即可写出An、Bn的坐标.
(1)![]() ,它们的纵坐标都是3,
,它们的纵坐标都是3,
而横坐标依次为![]() .
.
因此,![]() ,即
,即![]()
![]() ,它们的纵坐标都是0,
,它们的纵坐标都是0,
而横坐标依次是![]() ,
,
因此,![]() ,即
,即![]() ;
;
(2)由上题规律可知An的纵坐标总为3,横坐标为2n,Bn的纵坐标总为0,横坐标为2n+1.
所以An(2n,3),Bn(2n+1,0).
故答案分别为![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目