题目内容
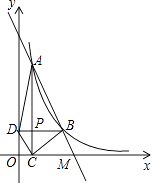
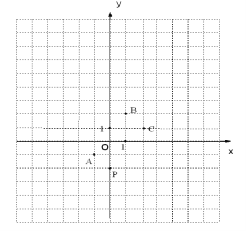
【题目】如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,….如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:
(2)求经过第2010次跳动之后,棋子落点的位置。
【答案】(1) M(-2,0),N(4,4);(2)(0,-2).
【解析】
(1)点P关于点A的对称点M,即是连接PA延长到M使PA=AM,所以M的坐标是M(-2,0),点M关于点B的对称点N处,即是连接PB延长到N使PB=BN,所以N的坐标是N(4,4);
(2)棋子跳动3次后又回点P处,利用这个循环的规律就可以得到棋子落点处的坐标.
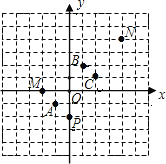
解:(1)首先发现点P的坐标是(0,-2),第一次跳到点P关于A点的对称点M处是(-2,0),跳到点M关于点B的对称点N处是(4,4);
(2)由(1)得出:则第三次再跳到点N关于点C的对称点处是(0,-2)…,发现3次一循环.又2010÷3=670,则第2010次跳动之后,棋子落点的坐标与点P坐标相同,落在了(0,-2)处.

练习册系列答案
相关题目