题目内容
【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
【答案】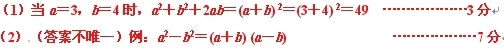
【解析】
(1)将a2+b2+2ab利用完全平方公式分解因式后,把已知条件代入求值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,都能使所得的多项式因式分解,先对所选的整式进行因式分解,然后将已知条件代入求值即可.
解:(1)当a=3,b=4时,a2+b2+2ab=(a+b)2=49;
(2)答案不唯一,
若选a2,b2,则a2-b2=(a+b)(a-b);
若选a2,2ab,则a2±2ab=a(a±2b);
若选b2,2ab,则b2+2ab=b(b±2a).

练习册系列答案
相关题目