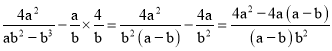题目内容
【题目】如图所示,平面直角坐标的原点是等边三角形的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
【答案】C
【解析】
△ABC绕点O顺时针旋转一周需6秒,而2017=6×336+1,所以第2017秒时,点A旋转到点A′,如图,则∠AOA′=60°,OA=OA′=1,作A′H⊥x轴于H,然后通过解直角三角形求出A′H和OH即可得到A′点的坐标.
∵360°÷60°=6,
2017=6×336+1,
∴第2017秒时,点A旋转到点A′,如图,
∠AOA′=60°,OA=OA′=1,
作A′H⊥x轴于H,
∵∠A′OH=30°,
∴A′H=![]() OA′=
OA′=![]() ,OH=
,OH=![]() A′H=
A′H=![]() ,
,
∴A′(![]() ,
,![]() ).
).

故答选:C
本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.