题目内容
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.
(1)你添加的条件是
(2)在(1)的条件下,不再添加辅助线和字母,证明DE=DF
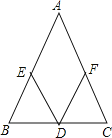
【答案】(1) AB=AC(答案不唯一);(2)证明见解析.
【解析】
(1)答案不唯一,若添加AB=AC,根据AB=AC,推出∠B=∠C,根据ASA证出△BED和△CFD全等即可;或添加∠B=∠C,根据ASA证出△BED和△CFD全等即可;添加∠BED=∠CDF,根据AAS即可推出△BED和△CFD全等;根据∠AED=∠AFD推出∠B=∠C,根据ASA证△BED≌△CFD即可;
(2)根据(1)中添加的条件结合三角形全等的判定方法进行证明即可.
(1)答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD,或∠AED=∠AFD等;
(2)①若添加AB=AC,证明如下:
∵AB=AC,
∴∠B=∠C,
在△BED和△CFD中,
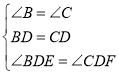 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
②若添加∠B=∠C,证明如下:
在△BED和△CFD中,
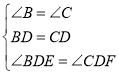 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
③若添加∠BED=∠CFD,证明如下:
在△BED和△CFD中,
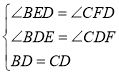 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF;
④若添加∠AED=∠AFD,证明如下:
∵∠AED=∠AFD,∠AED=∠B+∠BDE,∠AFD=∠C+∠CDF,
又∵∠BDE=∠CDF,
∴∠B=∠C,
在△BED和△CFD中,
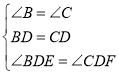 ,
,
∴△BED≌△CFD(ASA),
∴DE=DF.

【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?