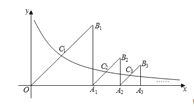
题目内容
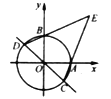
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是平行四边形.现将
是平行四边形.现将![]() 沿
沿![]() 轴方向平移
轴方向平移![]() 个单位,得到
个单位,得到![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
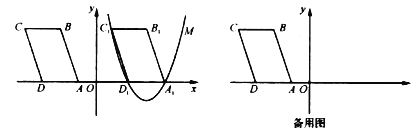
(1)若抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,求抛物线
,求抛物线![]() 的解析式;
的解析式;
(2)抛物线![]() 的顶点为
的顶点为![]() ,若以
,若以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积等于
为顶点的三角形的面积等于![]() 的面积的一半,求
的面积的一半,求![]() 的值;
的值;
(3)在(2)的条件下,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出点
?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)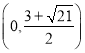 或
或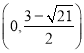 .
.
【解析】
(1)根据题意,先求出a的值,然后得到二次函数的解析式,然后得到平移后的解析式;
(2)根据题意,先求出直线![]() 的解析式,然后根据面积公式,即可得到答案;
的解析式,然后根据面积公式,即可得到答案;
(3)点A、C1、E作圆Q,则点Q在AC1的中垂线上,设点Q(m,![]() ),则求出m=1,然后根据勾股定理,即可求出t的值.
),则求出m=1,然后根据勾股定理,即可求出t的值.
解:(1)由题意得,![]() ,
,![]() ,
,
∴设过点![]() 的抛物线的解析式为:
的抛物线的解析式为:![]() ,
,
把![]() 代入
代入![]() ,
,
得![]() .
.
∴![]() .
.
∵平移之后过点![]() 、
、![]() 、
、![]() 的抛物线的顶点坐标
的抛物线的顶点坐标![]() .
.
∴抛物线![]() 的解析式为
的解析式为![]() .
.
(2)由题意得,平移![]() 个单位后,
个单位后,![]() ,
,![]() .
.
设直线![]() :
:![]() ,把点
,把点![]() ,
,![]() 代入,
代入,
得![]() ,
,
∴![]() .
.
令![]() ,得
,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() .
.
(3)存在,理由:
由(2)知点C(-1,3),点A(-1,0),则AC⊥x轴,

故点A、C1、E作圆Q,则点Q在AC1的中垂线上,设点Q(m,![]() ),
),
则此时,∠C1PA=∠C1EA,
由QC1=QE得:(m+1)2+(3-![]() )2=(m-1)2+(1+
)2=(m-1)2+(1+![]() )2,
)2,
解得:m=1,
则点Q(1,![]() ),设点P(0,t),
),设点P(0,t),
由QP=QE得:1+(![]() -t)2=(
-t)2=(![]() )2,
)2,
解得:![]() ,
,
故点P的坐标为: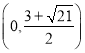 或
或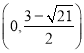 .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?