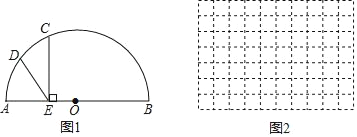题目内容
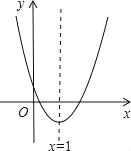
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝1，下列结论中：①abc＞0；②2a+b＝0；③3|a|＜2|b|；④b2﹣4ac＜0；⑤4a+2b+c＞0；⑥a+b≤n（an+b）（n为一切实数），其中正确的是______．
【答案】②③④⑤
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
①函数的对称轴在y轴右侧，则ab＜0，而c＞0，故abc＞0错误，不符合题意；
②函数的对称轴为：x＝﹣
＝1，即b＝﹣2a，故2a+b＝0正确，符合题意；
③由②知b＝﹣2a，3a+2b＝﹣a＜0，而a＞0，b＜0，故3|a|＜2|b|为3a+2b＜0，正确，符合题意；
④抛物线与x轴有两个交点，故b2﹣4ac＜0正确，符合题意；
⑤当x＝2时，y＝4a+2b+c＞0，正确，符合题意；
⑥函数在x＝1时，取得最小值，故a+b+c≤n（an+b）+c（n为一切实数），故a+b≤n（an+b）（n为一切实数）正确，符合题意；
故答案为：②③④⑤．
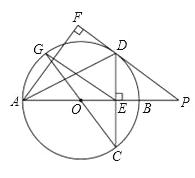
名校课堂系列答案
【题目】如图1，AB为半圆O的直径，半径的长为4cm，点C为半圆上一动点，过点C作CE⊥AB，垂足为点E，点D为弧AC的中点，连接DE，如果DE=2OE，求线段AE的长．
小何根据学习函数的经验，将此问题转化为函数问题解决．
小华假设AE的长度为xcm，线段DE的长度为ycm．
（当点C与点A重合时，AE的长度为0cm），对函数y随自变量x的变化而变化的规律进行探究．
下面是小何的探究过程，请补充完整：（说明：相关数据保留一位小数）．
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 |
| 5.8 | 5.7 |
当x=6cm时，请你在图中帮助小何完成作图，并使用刻度尺度量此时线段DE的长度，填写在表格空白处：
（2）在图2中建立平面直角坐标系，描出补全后的表中各组对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象解决问题，当DE=2OE时，AE的长度约为 cm．
