ћвƒњƒЏ»Ё
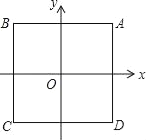
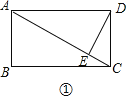
°Њћвƒњ°њґ®“е£Ї»зєы“їЄцЋƒ±я–ќіж‘Џ“їћхґ‘љ«ѕя£ђ єµ√’вћхґ‘љ«ѕя «Ћƒ±я–ќƒ≥Ѕљ±яµƒ±»јэ÷–ѕо£ђ‘т≥∆’вЄцЋƒ±я–ќќ™°∞…ЅЅЅЋƒ±я–ќ°±£ђ’вћхґ‘љ«ѕя≥∆ќ™°∞ЅЅѕя°±£Ѓ»зЌЉ1£ђЋƒ±я–ќABCD÷–£ђAB=AC=AD£ђ¬ъ„гAC2=ABAD£ђЋƒ±я–ќABCD «…ЅЅЅЋƒ±я–ќ£ђAC «ЅЅѕя£Ѓ
£®1£©“‘ѕ¬ЋµЈ®’э»Јµƒ «______£®ћо–і–тЇ≈£©
Ґў’эЈљ–ќ≤їњ…ƒ№ «…ЅЅЅЋƒ±я–ќ£ї
ҐЏЊЎ–ќ÷–іж‘Џ…ЅЅЅЋƒ±я–ќ£ї
Ґџ»ф“їЄцЅв–ќ «…ЅЅЅЋƒ±я–ќ£ђ‘т±Ў”–“їЄцƒЏљ« «60°г£Ѓ
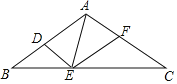
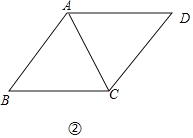
£®2£©»зЌЉ2£ђЋƒ±я–ќABCD÷–£ђAD°ќBC£ђ°ѕABC=90°г£ђAD=9£ђAB=12£ђCD=20£ђ≈–ґѕƒƒ“їћхѕяґќ «Ћƒ±я–ќABCDµƒЅЅѕя£њ«лƒг„ч≥ц≈–ґѕ≤ҐЋµ√чјн”…£Ѓ
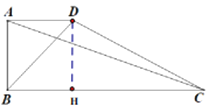
£®3£©»зЌЉ3£ђAC «…ЅЅЅЋƒ±я–ќABCDµƒќ®“їЅЅѕя£ђ°ѕABC=90°г£ђ°ѕD=60°г£ђAB=4£ђBC=2£ђ«л÷±љ”–і≥цѕяґќADµƒ≥§£Ѓ
°Њір∞Є°њ(1)Ґў°ҐҐџ£ї(2)![]() ќ™Ћƒ±я–ќ
ќ™Ћƒ±я–ќ![]() µƒЅЅѕя£ї(3)
µƒЅЅѕя£ї(3)![]() .
.
°Њљвќц°њ
£®1£©ЄщЊЁ…ЅЅЅЋƒ±я–ќµƒґ®“е“ї“ї≈–ґѕЉіњ…£Ѓ
£®2£©»зЌЉ2÷–£ђ„чDH°ЌBC”ЏH£Ѓ«у≥цBD£ђACЉіњ…≈–ґѕ£Ѓ
£®3£©ѕл∞мЈ®÷§√ч°чADC «µ»±я»эљ«–ќЉіњ…љвЊцќ ћв£Ѓ
љв£Ї(1) Ґў…и’эЈљ–ќµƒ±я≥§ќ™a£ђ‘тґ‘љ«ѕя≥§ќ™![]() a£ђ
a£ђ
![]() £ђ
£ђ
°а’эЈљ–ќ≤їњ…ƒ№ «…ЅЅЅЋƒ±я–ќ£Ѓє Ґў’э»Ј
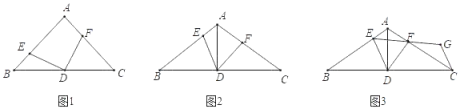
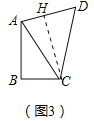
ҐЏ»зЌЉҐў÷–£ђЋƒ±я–ќABCD «ЊЎ–ќ£ђAE°ЌAC”ЏE£ђ≤їЈЅ…иЊЎ–ќ «…ЅЅЅЋƒ±я–ќ£Ѓ
‘тAC2=ADCD£ђ
![]() £ђ
£ђ
°аDE=AC£ђ
°яAC£ЊAD£ЊDE£ђѕ‘»ї”лDE=AC√ђґ№£ђЉў…и≤ї≥…ЅҐ£ђ
°аЊЎ–ќ≤їњ…ƒ№ «…ЅЅЅЋƒ±я–ќ£ђє ҐЏінќу£Ѓ
Ґџ»зЌЉҐЏ÷–£ђЋƒ±я–ќABCD «Ѕв–ќ£ђ
°яЋƒ±я–ќABCґЉ «…ЅЅЅЋƒ±я–ќ£ђ
≤їЈЅ…иAC2=ADCD£ђ
°яЋƒ±я–ќABCD «Ѕв–ќ£ђ
°аAD=CD£ђ
°аAC=AD=CD£ђ
°а°чADC «µ»±я»эљ«–ќ£ђ
°а°ѕD=60°г£ђ
°а»ф“їЄцЅв–ќ «…ЅЅЅЋƒ±я–ќ£ђ‘т±Ў”–“їЄцƒЏљ« «60°г£Ѓє Ґџ’э»Ј£Ѓ
є ір∞Єќ™ҐўҐџ
(2)єэµг![]() „ч
„ч![]() ”Џµг
”Џµг![]() £ђ
£ђ
°я![]() £ђ
£ђ![]() £ђ°а
£ђ°а![]()
°а![]() £ђ°аЋƒ±я–ќ
£ђ°аЋƒ±я–ќ![]() ќ™ЊЎ–ќ
ќ™ЊЎ–ќ
°я![]() £ђ
£ђ![]() £ђ
£ђ
°а![]() £ђ
£ђ![]() £ђ
£ђ![]() £Ѓ
£Ѓ
”÷°я![]() £ђ
£ђ![]()
°а![]() £ђ
£ђ![]()
іЋ ±![]() £ђ
£ђ![]()
°а![]() £ђЉі
£ђЉі![]() ќ™Ћƒ±я–ќ
ќ™Ћƒ±я–ќ![]() µƒЅЅѕя£Ѓ
µƒЅЅѕя£Ѓ
(3) »зЌЉ3÷–£ђ„чCH°ЌAD”ЏH£Ѓ
°яDH=CDcos°ѕD£ђCH=CDsin°ѕD£ђAH=AD-CDcos°ѕD£ђ
°аAC2=AH2+CH2=£®AD-CDcos°ѕD£©2+£®CDsin°ѕD£©2
=AD2+CD2-2ADCDcos°ѕD
=AD2+CD2-ADCD£ђ
°яAC2=ADCD£ђ
°аAD2-2ADCD+CD2=0£ђ
°а£®AD-CD£©2=0£ђ
°аAD=CD£ђ°я°ѕD=60°г£ђ
°а°чACD «µ»±я»эљ«–ќ£ђ
![]() .
.

°Њћвƒњ°њƒ≥…ћ≥°Јю„∞≤њќ™ЅЋµчґѓ”™“µ‘±µƒїэЉЂ–‘£ђЊцґ® µ––ƒњ±кє№јн£ђЄщЊЁƒњ±кЌк≥…µƒ«йњцґ‘”™“µ‘±љш–– µ±µƒљ±јш£Ѓќ™ЅЋ»Јґ®“їЄц µ±µƒ‘¬ѕъ џƒњ±к£ђ…ћ≥°Јю„∞≤њЌ≥Љ∆ЅЋ√њќї”™“µ‘±‘Џƒ≥‘¬µƒѕъ џґо£®µ•ќї£ЇЌт‘™£©£ђ эЊЁ»зѕ¬£Ї
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
ґ‘’в30Єц эЊЁ∞і„йЊа3љш––Ј÷„й£ђ≤Ґ’ыјн°Ґ√и цЇЌЈ÷ќц»зѕ¬£Ѓ
∆µ эЈ÷≤Љ±н
„й±р | “ї | ґю | »э | Ћƒ | ќе | Ѕщ | ∆я |
ѕъ џґо |
|
|
|
|
|
|
|
∆µ э | 7 | 9 | 3 |
| 2 |
| 2 |
эЊЁЈ÷ќц±н
∆љЊщ э | ÷Џ э | ÷–ќї э |
20.3 |
| 18 |
«лЄщЊЁ“‘…ѕ–≈ѕҐљвірѕ¬Ѕ–ќ ћв£Ї
£®1£©ћоњ’£Їa=°°°°£ђb=°°°°£ђc=°°°°£ї
£®2£©»фљЂ‘¬ѕъ џґо≤їµЌ”Џ25Ќт‘™»Јґ®ќ™ѕъ џƒњ±к£ђ‘т”–°°°°ќї”™“µ‘±їсµ√љ±јш£ї
£®3£©»фѕл»√“ї∞л„󔓵ƒ”™“µ‘±ґЉƒ№іпµљѕъ џƒњ±к£ђƒг»ѕќ™‘¬ѕъ џґоґ®ќ™ґа…ўЇѕ £њЋµ√чјн”…£Ѓ